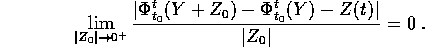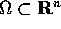 un aperto,
un aperto, 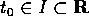 e
e
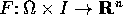 un campo vettoriale (anche dipendente
dal tempo) di classe
un campo vettoriale (anche dipendente
dal tempo) di classe 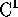 . Allora esiste un intorno di
. Allora esiste un intorno di
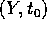 in
in 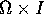 su cui il flusso integrale
su cui il flusso integrale 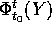 dell'equazione differenziale
dell'equazione differenziale
Sommario Il flusso integrale, come applicazione tra le condizioni iniziali ed i valori assunti dalle soluzioni ad un tempo fisso, è un diffeomorfismo, che si può calcolare risolvendo l'equazione alle variazioni.
Teorema di differenziabilità del flusso :
Siano 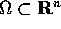 un aperto,
un aperto, 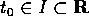 e
e
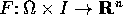 un campo vettoriale (anche dipendente
dal tempo) di classe
un campo vettoriale (anche dipendente
dal tempo) di classe 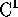 . Allora esiste un intorno di
. Allora esiste un intorno di
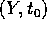 in
in 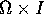 su cui il flusso integrale
su cui il flusso integrale 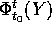 dell'equazione differenziale
dell'equazione differenziale

è una funzione 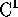 di tutte le variabili; inoltre esistono e sono
continue le derivate miste del tipo
di tutte le variabili; inoltre esistono e sono
continue le derivate miste del tipo

Dimostrazione:
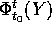 è continua rispetto a t e
Y; inoltre la continuità della derivata temporale segue da quella
del campo F, in quanto
è continua rispetto a t e
Y; inoltre la continuità della derivata temporale segue da quella
del campo F, in quanto
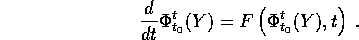
Sia ora 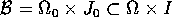 un compatto contenente
un compatto contenente 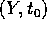 sul quale sono definiti
sul quale sono definiti 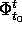 e le sue derivate. Dimostreremo che la derivata spaziale
e le sue derivate. Dimostreremo che la derivata spaziale 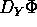 del flusso
del flusso
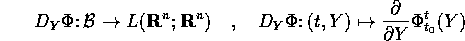
(ovvero la sua matrice jacobiana) è continua in un intorno di
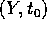 perché è un sistema fondamentale di soluzioni
dell'equazione alle variazioni
perché è un sistema fondamentale di soluzioni
dell'equazione alle variazioni
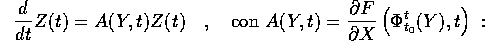
in altri termini, la soluzione Z(t) dell'equazione alle variazioni con
condizione iniziale 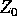 è la derivata spaziale del flusso
è la derivata spaziale del flusso 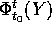 in direzione
in direzione 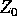 . Allora la continuità in t e la
dipendenza continua da Y di
. Allora la continuità in t e la
dipendenza continua da Y di 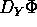 conseguono dalle proprietà
delle soluzioni
conseguono dalle proprietà
delle soluzioni 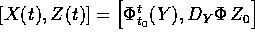 del problema
del problema
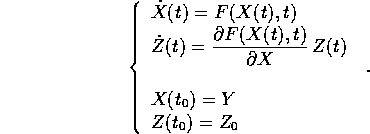
Si noti inoltre che le componenti di 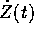 sono le derivate
miste del flusso integrale, e la loro continuità segue
dall'equazione.
sono le derivate
miste del flusso integrale, e la loro continuità segue
dall'equazione.
Infatti, il problema
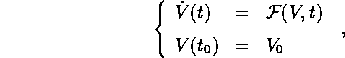
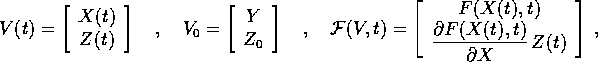
ammette soluzione in un intorno 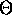 di
di 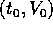 per l'uniforme
lipschitzianità di
per l'uniforme
lipschitzianità di 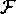 (che ha componenti uniformemente lipschitziane).
(che ha componenti uniformemente lipschitziane).
Mostriamo dunque che Z(t) coincide con 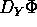 , ovvero che
, ovvero che
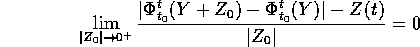
uniformemente in un intorno di 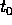 : il risultato si ottiene
maggiorando il numeratore del rapporto incrementale ed applicando il
lemma di Gronwall. Scriviamo le funzioni che compaiono
nell'espressione precedente come
: il risultato si ottiene
maggiorando il numeratore del rapporto incrementale ed applicando il
lemma di Gronwall. Scriviamo le funzioni che compaiono
nell'espressione precedente come
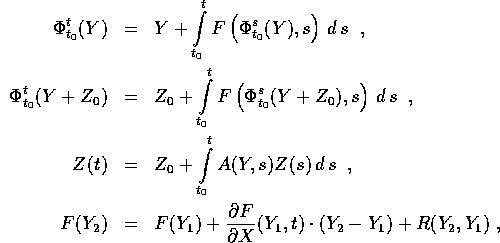
dove 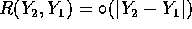 è un infinitesimo di ordine
superiore a
è un infinitesimo di ordine
superiore a 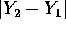 uniformemente rispetto a t nel compatto
uniformemente rispetto a t nel compatto 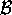 ; in particolare, per una opportuna costante K>0, in
; in particolare, per una opportuna costante K>0, in  si
ha, applicando il teorema di
continuità del flusso ,
si
ha, applicando il teorema di
continuità del flusso ,
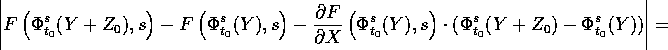
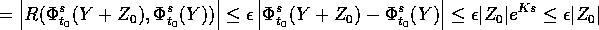
per 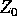 sufficientemente piccolo.
Allora
sufficientemente piccolo.
Allora
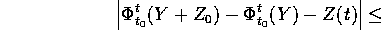
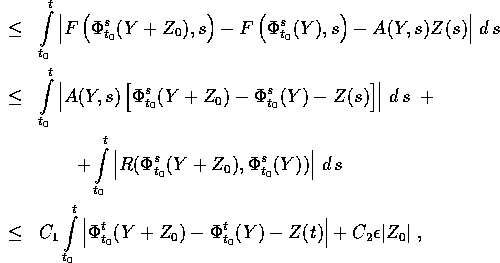
dove
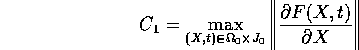
e 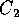 dipende
dall'ampiezza di
dipende
dall'ampiezza di 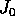 . Per il lemma di Gronwall, infine, si ottiene
. Per il lemma di Gronwall, infine, si ottiene
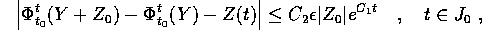
da cui, per l'arbitrarietà di  , discende
, discende