



Next: A TEOREMI DI ESISTENZA
Up: 9 NON INTEGRABILITÀ E
Previous: 9.3 NON INTEGRABILITÀ SECONDO
Sommario Discutiamo, senza conclusioni precise, la nozione di
caos, che dovrebbe descrivere le proprietà qualitative delle
orbite di sistemi hamiltoniani non integrabili, che non sono
rappresentabili mediante serie di Fourier. Vengono esaminate
due possibili definizioni, basate l'una sugli esponenti di
Lyapounov, l'altra sulla chiusura topologica delle orbite:
entrambe presentano dei problemi di non facile soluzione.
Se un sistema dinamico hamiltoniano non è integrabile, ed è dotato
di orbite con esponenti di Lyapounov positivi, che cosa si può dire
delle sue soluzioni? Non disponendo di una formula analitica (né
di una serie di Fourier) per descrivere il flusso
integrale, e neppure di un procedimento di approssimazione numerica
affidabile, i metodi tradizionali di descrizione delle soluzioni
devono essere abbandonati, o almeno usati solo entro limiti ben
precisi (per esempio, per tempi non troppo più lunghi del
tempo di Lyapounov ).
Ciò che si vorrebbe è una definizione (o anche più d'una)
soddisfatta dal comportamento di orbite di questo tipo, o almeno di
una frazione significativa di queste, che possa essere utilizzata per
costruire una nuova teoria qualitativa. Le definizioni di questa
classe impiegano di solito il nome di caos ; non esiste però
una definizione di caos che, considerata completamente
soddisfacente, sia comunemente accettata dai ricercatori
impegnati oggi in questo campo. Anziché dare la nostra definizione,
preferiamo dare un'idea dei problemi che sorgono nel cercare di
individuare la definizione ``buona''.
Una prima definizione di orbita caotica potrebbe richiedere che
esista almeno un esponente di Lyapounov positivo. Indubbiamente la
dipendenza critica dalla condizione iniziale è una
proprietà molto importante; per di più esiste almeno un
procedimento numerico di approssimazione che consente di ricavare un
valore indicativo del massimo esponente di Lyapounov.
Questa definizione ha però due difetti. Il primo è illustrato
dall'equazione del pendolo: 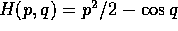 : il punto di sella
in
: il punto di sella
in 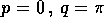 ha una coppia di esponenti di Lyapounov reali e di
segno opposto; si può mostrare che anche le separatrici hanno
esponenti di Lyapounov non nulli. Ciononostante il sistema è
integrabile, e variabili azione-angolo possono essere definite
ovunque, salvo che sulle separatrici; tutte le orbite sono calcolabili
per quadratura, anche quelle sulle separatrici. A parte il fatto che
una conoscenza imperfetta delle condizioni iniziali, o l'uso di un
integratore numerico poco accurato, potrebbe creare problemi nel
predire l'andamento a lungo termine di una soluzione molto vicina alla
separatrice, non c'è nessuna forma di imprevedibilità
nell'andamento qualitativo delle soluzioni. Quindi la presenza di un
esponente di Lyapounov positivo non basta a definire il caos.
ha una coppia di esponenti di Lyapounov reali e di
segno opposto; si può mostrare che anche le separatrici hanno
esponenti di Lyapounov non nulli. Ciononostante il sistema è
integrabile, e variabili azione-angolo possono essere definite
ovunque, salvo che sulle separatrici; tutte le orbite sono calcolabili
per quadratura, anche quelle sulle separatrici. A parte il fatto che
una conoscenza imperfetta delle condizioni iniziali, o l'uso di un
integratore numerico poco accurato, potrebbe creare problemi nel
predire l'andamento a lungo termine di una soluzione molto vicina alla
separatrice, non c'è nessuna forma di imprevedibilità
nell'andamento qualitativo delle soluzioni. Quindi la presenza di un
esponente di Lyapounov positivo non basta a definire il caos.
Il secondo problema è posto dall'esempio del problema dei tre
corpi. Senza entrare nei dettagli, che apparterrebbero ad un corso di
Meccanica Celeste, si può comprendere intuitivamente che un terzo
corpo di massa piccola (diciamo una cometa) che abbia degli incontri
ravvicinati con uno dei due corpi più grandi (diciamo Giove), può
essere spedito, per effetto di questi incontri, su una traiettoria
illimitata simile ad una traiettoria iperbolica del problema
dei due corpi cometa-Sole. Usando questa somiglianza (cioè una
teoria perturbativa), ed il risultato del problema che discuteremo qui
sotto, si può
mostrare che una simile orbita di espulsione ha esponenti di Lyapounov
tutti nulli. Perciò ci sono orbite con comportamento estremamente
irregolare ed estremamente instabile, con sequenze di incontri
ravvicinati terminate dall'espulsione, che vorremmo chiamare caotiche,
ma che non sono coperte da una definizione basata solo sugli esponenti
di Lyapounov.
Problema
Dimostrare che gli esponenti di Lyapounov
di un'orbita iperbolica del problema dei due corpi sono tutti nulli.
Un altro tipo di definizione potrebbe essere basata sulla
transitività topologica, cioè sulla natura dell'insieme che si
ottiene come chiusura topologica di un'orbita. Le orbite di un sistema
integrabile a due gradi di libertà o sono periodiche, quindi formano
un insieme chiuso , oppure sono dense in un toro  . Le orbite
caotiche non sono confinate né in un toro, né in alcun altra
varietà invariante della stessa dimensione (perché non ci sono
``abbastanza'' integrali primi). Si potrebbe allora definire una
regione caotica come un insieme dello spazio delle fasi che
coincide con la chiusura di ogni sua orbita. Chiaramente però
occorre che questo insieme sia ``più grande'' di un toro invariante
del tipo presente nei sistemi integrabili. Per esempio si potrebbe
richiedere che la regione caotica riempia l'insieme di livello
definito dal solo integrale primo, cioè dalla hamiltoniana; oppure
che sia un sottoinsieme aperto dell'insieme di livello.
. Le orbite
caotiche non sono confinate né in un toro, né in alcun altra
varietà invariante della stessa dimensione (perché non ci sono
``abbastanza'' integrali primi). Si potrebbe allora definire una
regione caotica come un insieme dello spazio delle fasi che
coincide con la chiusura di ogni sua orbita. Chiaramente però
occorre che questo insieme sia ``più grande'' di un toro invariante
del tipo presente nei sistemi integrabili. Per esempio si potrebbe
richiedere che la regione caotica riempia l'insieme di livello
definito dal solo integrale primo, cioè dalla hamiltoniana; oppure
che sia un sottoinsieme aperto dell'insieme di livello.
Per decidere se una definizione di questo tipo è applicabile nei
casi più comuni e più interessanti, occorre procurarsi qualche
esempio di sistema ``caotico''. Benché gli esempi non manchino, i
metodi numerici necessari per mettere in evidenza il caos sono, nella
maggior parte dei casi, complicati e di uso difficile. Nella prossima
sottosezione svilupperemo quindi un metodo per procurarsi esempi molto
semplici da calcolare.
Sia 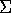 una ipersuperficie regolare dello spazio delle fasi
(P,Q),
cioè un sottoinsieme definito da una sola equazione G(P,Q)=0 con
G di classe
una ipersuperficie regolare dello spazio delle fasi
(P,Q),
cioè un sottoinsieme definito da una sola equazione G(P,Q)=0 con
G di classe  e con
e con 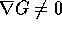 in ogni punto di
in ogni punto di
 . Supponiamo che
. Supponiamo che 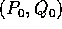 sia un punto di
sia un punto di 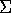 per il
quale passa trasversalmente la soluzione del sistema
hamiltoniano definito da H(P,Q), cioè
per il
quale passa trasversalmente la soluzione del sistema
hamiltoniano definito da H(P,Q), cioè
allora la ipersuperficie  resterà trasversale al sistema
dinamico per tutti i punti di un intorno di
resterà trasversale al sistema
dinamico per tutti i punti di un intorno di  in
in 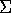 ;
si dice che
;
si dice che 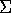 è una
sezione locale
(questa definizione è analoga a quella di sezione locale
per un sistema dinamico piano).
è una
sezione locale
(questa definizione è analoga a quella di sezione locale
per un sistema dinamico piano).
Allora la soluzione con condizione iniziale 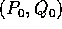 lascia
lascia
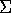 per t>0 (anche per t<0). Supponiamo che dopo un certo
tempo
per t>0 (anche per t<0). Supponiamo che dopo un certo
tempo 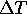 la soluzione torni ad incontrare
la soluzione torni ad incontrare 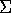 in
in
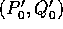 : si intende che questo sia il ``primo ritorno'', cioè
per
: si intende che questo sia il ``primo ritorno'', cioè
per 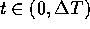 la soluzione non incontra
la soluzione non incontra 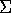 .
Supponiamo che anche questo secondo incontro sia trasversale, cioè
anche in
.
Supponiamo che anche questo secondo incontro sia trasversale, cioè
anche in 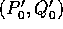 si abbia
si abbia 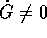 . Per il teorema di
continuità del flusso , tutte
le soluzioni con condizione iniziale (P,Q) che stanno su
. Per il teorema di
continuità del flusso , tutte
le soluzioni con condizione iniziale (P,Q) che stanno su 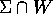 , con W un intorno abbastanza piccolo di
, con W un intorno abbastanza piccolo di 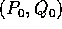 ,
incontreranno di nuovo
,
incontreranno di nuovo  in un punto (P',Q').
L'applicazione così definita è la
mappa di Poincaré
in un punto (P',Q').
L'applicazione così definita è la
mappa di Poincaré
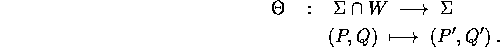
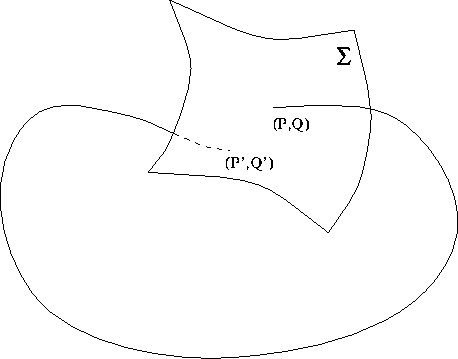
Figure 9.2: Mappa di Poincaré: data una ipersuperficie
che rappresenta una sezione locale, si manda ogni punto nel punto di
primo ritorno sull'ipersuperficie dell'orbita corrispondente.
Per il teorema di
differenziabilità del flusso , la mappa di Poincaré è un
diffeomorfismo tra due intorni di 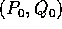 su
su 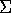 . Si
noti che la mappa di Poincarè conserva il valore della hamiltoniana.
. Si
noti che la mappa di Poincarè conserva il valore della hamiltoniana.
Un caso semplice della mappa di Poincaré si ottiene quando
le variabili Q sono variabili angolo: se consideriamo 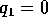 come ipersuperficie
come ipersuperficie 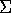 , e per esempio sappiamo che
, e per esempio sappiamo che 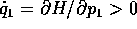 in ogni punto, allora
in ogni punto, allora
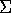 è trasversale al sistema dinamico in ogni punto, e
il primo ritorno è semplicemente il punto su ogni orbita in
cui
è trasversale al sistema dinamico in ogni punto, e
il primo ritorno è semplicemente il punto su ogni orbita in
cui 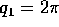 . Studiamo il caso con due gradi di libertà
per semplicità di notazione (la generalizzazione ad n
gradi di libertà è comunque ovvia): poiché la
hamiltoniana è conservata,
. Studiamo il caso con due gradi di libertà
per semplicità di notazione (la generalizzazione ad n
gradi di libertà è comunque ovvia): poiché la
hamiltoniana è conservata,
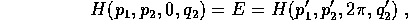
e da questa equazione si possono ricavare sia 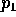 che
che 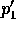 ,
per il teorema delle funzioni implicite (dal momento che
,
per il teorema delle funzioni implicite (dal momento che
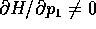 ). Perciò, fissato il valore
H=E della hamiltoniana, si può definire una
mappa di Poincaré ridotta
). Perciò, fissato il valore
H=E della hamiltoniana, si può definire una
mappa di Poincaré ridotta
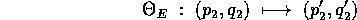
in cui il punto di primo ritorno appartiene all'orbita
che ha condizione iniziale con 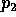 e
e 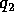 assegnati su
assegnati su
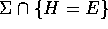 . In questo caso vale una proprietà molto forte:
. In questo caso vale una proprietà molto forte:
Teorema dei conseguenti :
La mappa di Poincaré ridotta è una trasformazione canonica .
Dimostrazione:
-
-
Ricavando
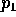 da
da 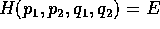 con il teorema della
funzione implicita, si ottiene la funzione delle altre
variabili
con il teorema della
funzione implicita, si ottiene la funzione delle altre
variabili 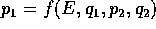 , le cui derivate parziali sono
, le cui derivate parziali sono
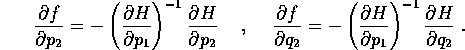
Definiamo allora l'hamiltoniana K come
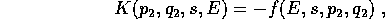
con variabile indipendente 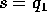 (in luogo del tempo)
e parametro E, per definire le equazioni di
Hamilton
(in luogo del tempo)
e parametro E, per definire le equazioni di
Hamilton
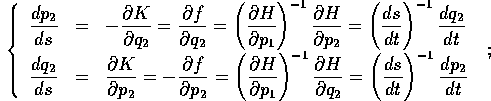
esse sono equivalenti a quelle originali, nel senso che la stessa
orbita è parametrizzata da 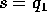 anziché da t.
anziché da t.
Le nuove equazioni di Hamilton sono state ottenute
``eliminando il tempo'' nelle equazioni originali.
Perciò la mappa di Poincaré ridotta si può considerare
come il flusso integrale da s=0 ad 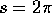 del sistema
hamiltoniano con hamiltoniana K. Per il teorema del
flusso canonico la mappa di Poincaré è quindi
canonica.
del sistema
hamiltoniano con hamiltoniana K. Per il teorema del
flusso canonico la mappa di Poincaré è quindi
canonica.
C.D.D.Nel caso a due gradi di libertà, 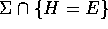 è una
superficie e, per riferirsi al teorema precedente, supponiamo che
è una
superficie e, per riferirsi al teorema precedente, supponiamo che
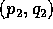 siano le sue coordinate: una
trasformazione canonica
conserva l'area . Quindi la mappa di Poincaré ridotta
definisce un sistema dinamico discreto conservativo , definito
in un sottoinsieme del piano
siano le sue coordinate: una
trasformazione canonica
conserva l'area . Quindi la mappa di Poincaré ridotta
definisce un sistema dinamico discreto conservativo , definito
in un sottoinsieme del piano 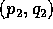 .
.
Se il sistema hamiltoniano di partenza fosse integrabile,
allora vi sarebbe un altro integrale primo Z(P,Q),
funzionalmente indipendente da H(P,Q), e la mappa di
Poincaré dovrebbe conservare anche questo; quindi la mappa
di Poincaré ridotta avrebbe un integrale primo , le
cui curve di livello sarebbero invarianti, cioè unione di
orbite. Se il sistema non è integrabile, le orbite della
mappa di Poincaré ridotta occupano insiemi del piano
``più grandi'' di curve.
Da questa relazione tra sistemi hamiltoniani a due gradi di
libertà e sistemi dinamici conservativi nel piano segue
che è possibile riconoscere il caos con un metodo grafico.
Basta seguire un'orbita della mappa di Poincaré ridotta, ed
osservare come si dispone nel piano.
La mappa di Poincaré ridotta introduce una relazione tra sistemi
dinamici conservativi nel
piano, e sistemi hamiltoniani a due gradi di libertà;
possiamo
utilizzare gli esempi dei primi come modello per i
comportamenti - integrabili o caotici - dei secondi.
Perciò possiamo usare una mappa standard
come esempio; nel seguito useremo ancora quella già studiata
nel Capitolo 4,
la mappa standard del pendolo .
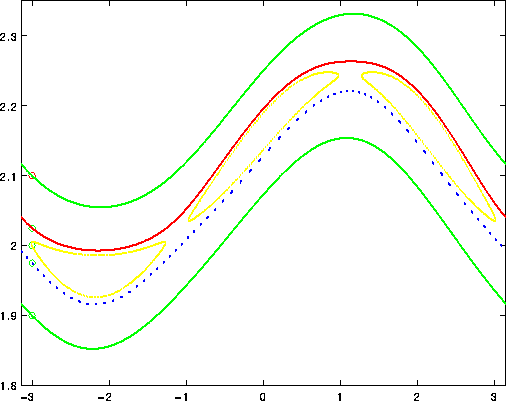
Figure 9.3: Particolare della mappa standard del pendolo
per il valore h=0.5: la maggior parte delle orbite sembra appartenere
a curve invarianti; tuttavia non c'è alcun aperto dello spazio delle
fasi in cui manchi il caos, con esponenti di Lyapounov positivi. Le
orbite caotiche sembrano``riempire'' sottili corone circolari comprese
tra due curve invarianti; per una visione d'insieme, si veda la Figura
4.4.
Osserviamo con un opportuno ingrandimento il risultato
degli esperimenti numerici che calcolano, per diversi valori del
parametro h, un lungo
tratto (migliaia di punti) di alcune orbite della mappa
standard del pendolo: si nota che nel fascio di curve
invarianti - che dominano per valori piccoli di h -
si formano delle isole di risonanza che generano nuove regioni
caotiche, a partire dalle
separatrici di orbite
periodiche con esponenti di Lyapounov positivi e negativi.
La conclusione, molto provvisoria ed empirica, di questo
esperimento, è che anche una definizione di caos basata
sulla transitività topologica non è del tutto adeguata,
specialmente per i sistemi hamiltoniani (e per i sistemi
discreti conservativi). Al contrario, le orbite caotiche
riempiono la parte dello spazio delle fasi lasciata libera da
un gran numero di curve invarianti (corrispondenti ai tori
invarianti nel caso hamiltoniano).
Semplici esperimenti numerici come questo, compiuti con i primi
calcolatori elettronici all'inizio degli anni '50, hanno stimolato
gli sviluppi di una nuova teoria dei sistemi dinamici hamiltoniani
non integrabili, ma aventi orbite sia caotiche sia regolari: si veda
[Arnold 86], Appendice 8.
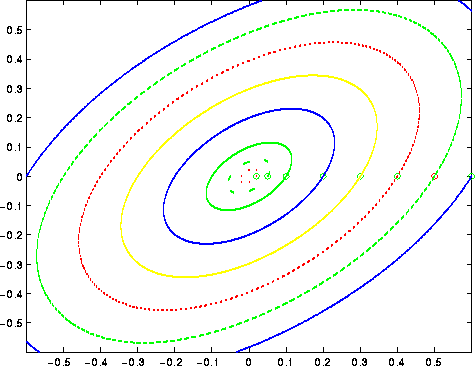
Figure 9.4: Particolare della mappa standard del pendolo
per il valore h=1: la maggior parte delle curve invarianti
è scomparsa, ma restano quelle che hanno
ampiezze di oscillazione piccole attorno al punto di equilibrio
stabile. Nemmeno in questo caso c'è transitività topologica; per
una veduta d'insieme, si veda la Figura 4.6.
\




Next: A TEOREMI DI ESISTENZA
Up: 9 NON INTEGRABILITÀ E
Previous: 9.3 NON INTEGRABILITÀ SECONDO
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
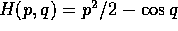 : il punto di sella
in
: il punto di sella
in 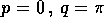 ha una coppia di esponenti di Lyapounov reali e di
segno opposto; si può mostrare che anche le separatrici hanno
esponenti di Lyapounov non nulli. Ciononostante il sistema è
integrabile, e variabili azione-angolo possono essere definite
ovunque, salvo che sulle separatrici; tutte le orbite sono calcolabili
per quadratura, anche quelle sulle separatrici. A parte il fatto che
una conoscenza imperfetta delle condizioni iniziali, o l'uso di un
integratore numerico poco accurato, potrebbe creare problemi nel
predire l'andamento a lungo termine di una soluzione molto vicina alla
separatrice, non c'è nessuna forma di imprevedibilità
nell'andamento qualitativo delle soluzioni. Quindi la presenza di un
esponente di Lyapounov positivo non basta a definire il caos.
ha una coppia di esponenti di Lyapounov reali e di
segno opposto; si può mostrare che anche le separatrici hanno
esponenti di Lyapounov non nulli. Ciononostante il sistema è
integrabile, e variabili azione-angolo possono essere definite
ovunque, salvo che sulle separatrici; tutte le orbite sono calcolabili
per quadratura, anche quelle sulle separatrici. A parte il fatto che
una conoscenza imperfetta delle condizioni iniziali, o l'uso di un
integratore numerico poco accurato, potrebbe creare problemi nel
predire l'andamento a lungo termine di una soluzione molto vicina alla
separatrice, non c'è nessuna forma di imprevedibilità
nell'andamento qualitativo delle soluzioni. Quindi la presenza di un
esponente di Lyapounov positivo non basta a definire il caos.
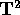 . Le orbite
caotiche non sono confinate né in un toro, né in alcun altra
varietà invariante della stessa dimensione (perché non ci sono
``abbastanza'' integrali primi). Si potrebbe allora definire una
regione caotica
. Le orbite
caotiche non sono confinate né in un toro, né in alcun altra
varietà invariante della stessa dimensione (perché non ci sono
``abbastanza'' integrali primi). Si potrebbe allora definire una
regione caotica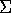 una ipersuperficie
una ipersuperficie e con
e con 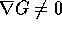 in ogni punto di
in ogni punto di
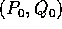 sia un punto di
sia un punto di 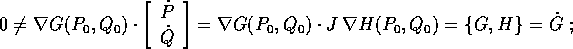
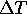 la soluzione torni ad incontrare
la soluzione torni ad incontrare 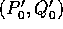 : si intende che questo sia il ``primo ritorno'', cioè
per
: si intende che questo sia il ``primo ritorno'', cioè
per 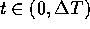 la soluzione non incontra
la soluzione non incontra 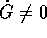 . Per il teorema di
. Per il teorema di
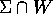 , con W un intorno abbastanza piccolo di
, con W un intorno abbastanza piccolo di 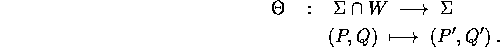

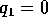 come ipersuperficie
come ipersuperficie 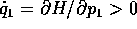 in ogni punto, allora
in ogni punto, allora
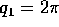 . Studiamo il caso con due gradi di libertà
per semplicità di notazione (la generalizzazione ad n
gradi di libertà è comunque ovvia): poiché la
hamiltoniana è conservata,
. Studiamo il caso con due gradi di libertà
per semplicità di notazione (la generalizzazione ad n
gradi di libertà è comunque ovvia): poiché la
hamiltoniana è conservata,
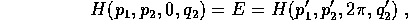
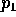 che
che 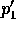 ,
per il teorema delle
,
per il teorema delle 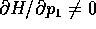 ). Perciò, fissato il valore
H=E della hamiltoniana, si può definire una
mappa di Poincaré ridotta
). Perciò, fissato il valore
H=E della hamiltoniana, si può definire una
mappa di Poincaré ridotta
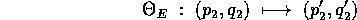
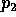 e
e 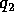 assegnati su
assegnati su
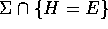 . In questo caso vale una proprietà molto forte:
. In questo caso vale una proprietà molto forte:
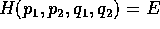 con il teorema della
funzione implicita, si ottiene la funzione delle altre
variabili
con il teorema della
funzione implicita, si ottiene la funzione delle altre
variabili 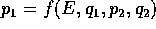 , le cui derivate parziali sono
, le cui derivate parziali sono
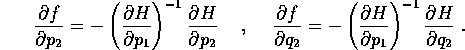
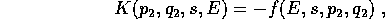
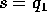 (in luogo del tempo)
e parametro E, per definire le equazioni di
Hamilton
(in luogo del tempo)
e parametro E, per definire le equazioni di
Hamilton
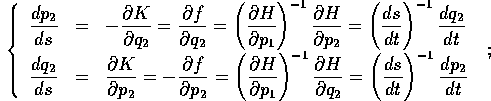
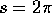 del sistema
hamiltoniano con hamiltoniana K. Per il teorema del
del sistema
hamiltoniano con hamiltoniana K. Per il teorema del
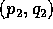 siano le sue coordinate: una
siano le sue coordinate: una

