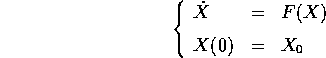
Sommario Gli esponenti di Lyapounov misurano il ritmo esponenziale di divergenza di orbite con condizioni iniziali vicine, generalizzando la definizione data nel caso dei punti di equilibrio. Nei sistemi hamiltoniani integrabili gli esponenti di Lyapounov sono zero. Se ci sono esponenti di Lyapounov positivi, anche le integrazioni numeriche accumulano l'errore di discretizzazione in modo esponenziale, e non possono essere impiegate per predire in modo affidabile l'evoluzione a lungo termine delle orbite.
Per ogni orbita di un sistema dinamico che risolve il problema alle condizioni iniziali
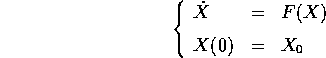
l'equazione alle variazioni è un'equazione differenziale lineare dipendente dal tempo, la cui soluzione è la matrice jacobiana del flusso integrale (che esiste per il teorema di differenziabilità del flusso :
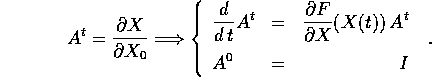
La matrice 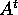 , soluzione di tale problema alle condizioni iniziali qua
sopra, è anche la matrice associata al flusso integrale (lineare)
dell'equazione alle variazioni, nel senso che la soluzione del
problema alle condizioni iniziali
, soluzione di tale problema alle condizioni iniziali qua
sopra, è anche la matrice associata al flusso integrale (lineare)
dell'equazione alle variazioni, nel senso che la soluzione del
problema alle condizioni iniziali
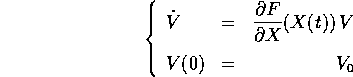
con 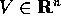 può essere espressa come
può essere espressa come

È quindi naturale chiedersi quale sarà il comportamento delle
soluzioni V(t) per 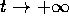 ; se interpretiamo l'equazione alle
variazioni come l'equazione del moto relativo linearizzata (vedi
Sezione 8.6), la soluzione V(t) descrive (al
primo ordine in |V(t)| )come la soluzione con condizione iniziale
; se interpretiamo l'equazione alle
variazioni come l'equazione del moto relativo linearizzata (vedi
Sezione 8.6), la soluzione V(t) descrive (al
primo ordine in |V(t)| )come la soluzione con condizione iniziale
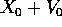 si allontana nel tempo da quella di riferimento (con
condizione iniziale
si allontana nel tempo da quella di riferimento (con
condizione iniziale  ).
).
Definizione:
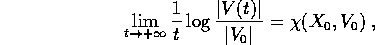
dove V(t) è la soluzione (con condizione iniziale 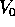 )
dell'equazione alle variazioni (relativa all'orbita con condizione iniziale
)
dell'equazione alle variazioni (relativa all'orbita con condizione iniziale
 ) associata al sistema dinamico.
) associata al sistema dinamico.
Per la linearità dell'equazione
alle variazioni, gli esponenti di Lyapounov dipendono in effetti
solamente dalla direzione di 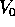 . Poiché inoltre si ottengono gli stessi
esponenti in corrispondenza
di condizioni iniziali in punti
. Poiché inoltre si ottengono gli stessi
esponenti in corrispondenza
di condizioni iniziali in punti  e
e 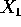 appartenenti alla
stessa traiettoria, si può parlare degli
esponenti di Lyapounov di un'orbita.
appartenenti alla
stessa traiettoria, si può parlare degli
esponenti di Lyapounov di un'orbita.
Esempio:
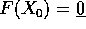 , per cui
, per cui 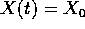 è un'orbita
corrispondente ad un punto di equilibrio. Allora l'equazione alle variazioni
è un'orbita
corrispondente ad un punto di equilibrio. Allora l'equazione alle variazioni
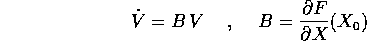
coincide con il sistema linearizzato, ed ha flusso integrale
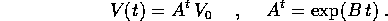
In questo caso gli autovalori di 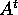 sono
sono 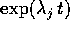 , dove
, dove
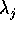 sono gli autovalori di B. Se
sono gli autovalori di B. Se 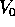 è
un autovettore di B con autovalore
è
un autovettore di B con autovalore 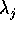 reale si trova
reale si trova
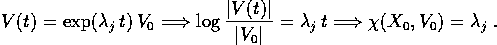
Per mezzo della forma canonica reale, si verifica che se 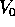 sta nella
parte reale degli autospazi di una coppia di autovalori complessi
coniugati
sta nella
parte reale degli autospazi di una coppia di autovalori complessi
coniugati 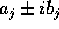 si ottiene
si ottiene 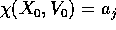 . In generale,
un vettore iniziale
. In generale,
un vettore iniziale 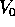 sarà combinazione lineare di autovettori
e autovettori generalizzati, quindi in
sarà combinazione lineare di autovettori
e autovettori generalizzati, quindi in 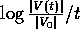 sarà dominante il contributo dell'autovalore con parte reale
massima.
sarà dominante il contributo dell'autovalore con parte reale
massima.
In conclusione, gli esponenti di Lyapounov dell'orbita  sono
tutte e sole le parti reali degli autovalori di B, cioè
coincidono con gli esponenti di Lyapounov definiti nel
caso particolare di un punto di equilibrio.
sono
tutte e sole le parti reali degli autovalori di B, cioè
coincidono con gli esponenti di Lyapounov definiti nel
caso particolare di un punto di equilibrio.
Problema
Supponiamo che X(t) sia un'orbita periodica di periodo
P. Allora la matrice di monodromia 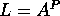 contiene tutte
le informazioni sugli esponenti di Lyapounov: mostrare che, se
contiene tutte
le informazioni sugli esponenti di Lyapounov: mostrare che, se
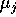 sono gli autovalori di L, allora gli esponenti di Lyapounov
dell'orbita X(t) sono
sono gli autovalori di L, allora gli esponenti di Lyapounov
dell'orbita X(t) sono 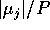 .
.
Esempio:
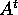 abbia un autovalore
abbia un autovalore 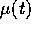 il cui autospazio
contenga
il cui autospazio
contenga 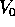 per ogni t. Allora
per ogni t. Allora
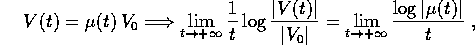
ed un eventuale esponente di Lyapounov misura la crescenza esponenziale dell'autovalore.
Benché questi esempi siano importanti, la definizione di
esponente di Lyapounov è più generale e vale per orbite
qualsiasi, anche in corrispondenza di comportamenti molti complicati
degli autospazi di A(t). Non è detto che per ogni condizione
iniziale  esistano degli esponenti di Lyapounov. Prima di tutto
occorre che
esistano degli esponenti di Lyapounov. Prima di tutto
occorre che  appartenga ad un'orbita , altrimenti il
limite per
appartenga ad un'orbita , altrimenti il
limite per 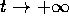 non avrebbe senso; ma anche per le orbite
può accadere che i limiti che definiscono gli esponenti non siano
convergenti.
non avrebbe senso; ma anche per le orbite
può accadere che i limiti che definiscono gli esponenti non siano
convergenti.
Consideriamo un sistema dinamico conservativo, per esempio sotto forma di equazioni di Hamilton :
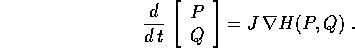
L'equazione alle variazioni ha in questo caso la forma particolare
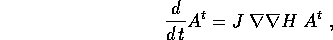
dove la matrice hessiana della funzione di Hamilton è calcolata
lungo la soluzione di riferimento. Per il teorema del
flusso canonico , la soluzione 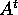 è una
matrice simplettica per ogni t, quindi (per il teorema di
Liouville ) ammette sempre coppie di autovalori del tipo
è una
matrice simplettica per ogni t, quindi (per il teorema di
Liouville ) ammette sempre coppie di autovalori del tipo
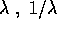 .
.
Esempio:
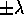 , e che perciò
gli esponenti di Lyapounov formano coppie del tipo
, e che perciò
gli esponenti di Lyapounov formano coppie del tipo 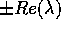 .
.
Si può dimostrare che la proprietà descritta in questo esempio,
cioè di avere per ogni esponente di Lyapounov positivo anche il
corrispondente negativo (e viceversa), vale per ogni orbita di un
sistema hamiltoniano. Perciò ci sono soltanto due casi: o gli
esponenti di Lyapounov sono tutti nulli, oppure ce ne sono sia di
positivi che di negativi. Nel secondo caso esiste almeno una direzione
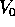 tale che un piccolo cambiamento nelle condizioni iniziali porta
ad una crescita esponenziale della distanza tra le due orbite, cioè
ad una dipendenza critica dalla condizione iniziale .
tale che un piccolo cambiamento nelle condizioni iniziali porta
ad una crescita esponenziale della distanza tra le due orbite, cioè
ad una dipendenza critica dalla condizione iniziale .
Teorema del moto ordinato : Se un sistema dinamico hamiltoniano è integrabile , allora non c'è dipendenza critica dalla condizione iniziale, nel senso che tutti gli esponenti di Lyapounov sono zero.
In effetti dimostreremo che per ogni condizione iniziale
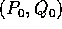 e per ogni vettore variazione iniziale
e per ogni vettore variazione iniziale
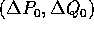 esiste ed è sempre zero il limite che
definisce l'esponente di Lyapounov.
esiste ed è sempre zero il limite che
definisce l'esponente di Lyapounov.
Dimostrazione:
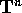 ,
parametrizzato da n
variabili angolo
,
parametrizzato da n
variabili angolo
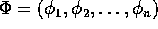 , e la dinamica sul toro
è un flusso di Kronecker
, e la dinamica sul toro
è un flusso di Kronecker
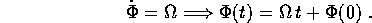
Inoltre esistono variabili azione-angolo (che includono,
oltre agli angoli 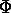 citati sopra, le variabili azione
citati sopra, le variabili azione
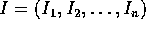 ) tali che le
) tali che le 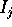 sono integrali primi, e
le frequenze proprie sono funzioni
sono integrali primi, e
le frequenze proprie sono funzioni
 delle sole I:
delle sole I: 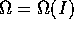
In queste condizioni, prendiamo una condizione iniziale 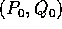 ed un vettore variazione iniziale
ed un vettore variazione iniziale 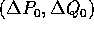 : a questi
corrisponde nelle coordinate
: a questi
corrisponde nelle coordinate 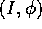 una condizione iniziale
una condizione iniziale
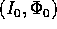 ed un vettore variazione
ed un vettore variazione 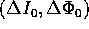 .
.
Il vettore variazione è un vettore tangente, per la cui trasformazione da un sistema di coordinate ad un altro si deve usare il differenziale in modo controvariante .
Calcoliamo la differenza tra due orbite, quella 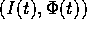 per
per
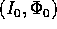 e quella
e quella 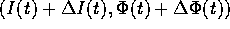 per
per 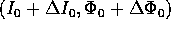 :
:
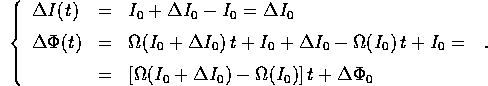
Da questa formula esplicita si vede che la distanza 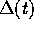 tra
le orbite cresce solo linearmente nel tempo (e solo
nelle direzioni lungo il toro), perciò
tra
le orbite cresce solo linearmente nel tempo (e solo
nelle direzioni lungo il toro), perciò 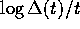 tende a
zero. Questo calcolo è stato eseguito usando le differenze tra le
orbite, anziché i vettori variazione (e quindi l'equazione
linearizzata); ma poiché il flusso integrale in questo caso è
lineare, è esattamente lo stesso.
tende a
zero. Questo calcolo è stato eseguito usando le differenze tra le
orbite, anziché i vettori variazione (e quindi l'equazione
linearizzata); ma poiché il flusso integrale in questo caso è
lineare, è esattamente lo stesso.
Si tratta ora di mostrare che gli esponenti di Lyapounov di una data
orbita non dipendono dal sistema di coordinate usato, ovvero che anche
nelle variabili (P,Q) sarebbero gli stessi che nelle variabili
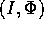 .
.
Ciascun toro 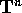 è compatto , perciò se si esegue un
cambiamento di coordinate che sia un diffeomorfismo su tale
compatto, la sua matrice jacobiana C avrà un massimo k della
norma uniforme ||C||. Applichiamo questo criterio al
cambiamento di coordinate dalle variabili azione-angolo alle
(P,Q): allora la lunghezza del vettore variazione nelle coordinate
(P,Q) sarà maggiorata da
è compatto , perciò se si esegue un
cambiamento di coordinate che sia un diffeomorfismo su tale
compatto, la sua matrice jacobiana C avrà un massimo k della
norma uniforme ||C||. Applichiamo questo criterio al
cambiamento di coordinate dalle variabili azione-angolo alle
(P,Q): allora la lunghezza del vettore variazione nelle coordinate
(P,Q) sarà maggiorata da 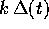 , e
, e
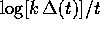 tende a zero.
tende a zero.
In effetti gli esponenti di Lyapounov non dipendono affatto dal sistema di coordinate usato, almeno finché il problema è circoscritto ad un insieme compatto.
Se il sistema dinamico non è integrabile, per calcolare le soluzioni si può ricorrere a qualche forma di approssimazione: per esempio all'integrazione numerica, usando uno dei molti metodi disponibili (tra cui quelli discussi nella Sezione 4.4). Il problema è che l'errore di troncamento accumulato cresce con il tempo, fino a rendere l'approssimazione discreta completamente differente dalla soluzione del sistema dinamico continuo.
Nel caso più semplice del metodo di Eulero , il teorema della convergenza del metodo di Eulero fornisce una stima dell'errore accumulato che presenta una crescita esponenziale con il tempo, con esponente dipendente dalla costante di Lipschitz del secondo membro.
Per altri metodi di integrazione più accurati, il termine costante che moltiplica l'esponenziale potrà essere molto più piccolo, ma rimane la divergenza dell'andamento esponenziale nel tempo della stima.
Una giustificazione per questo cattivo comportamento delle
approssimazioni numeriche può essere trovata nel teorema della
continuità del flusso (che a sua
volta discende dalla diseguaglianza di Gronwall ), per
il quale la crescita della distanza tra due orbite con condizioni
iniziali diverse è sempre stimata da un'esponenziale nel tempo, con
esponente contenente la costante di Lipschitz. In effetti il teorema
di continuità fornisce una maggiorazione degli esponenti di
Lyapounov. Di conseguenza, che nessun metodo di integrazione numerica può
evitare di accumulare l'errore in modo esponenziale, quando viene
applicato ad un sistema dinamico con esponenti di Lyapounov positivi:
supponiamo, come caso limite, che il metodo di discretizzazione
commetta un errore di modulo 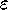 molto piccolo al primo
passo; se anche nei passi successivi
l'errore di troncamento locale
fosse nullo, sarebbe sufficiente seguire una nuova orbita con
condizioni iniziali differenti di
molto piccolo al primo
passo; se anche nei passi successivi
l'errore di troncamento locale
fosse nullo, sarebbe sufficiente seguire una nuova orbita con
condizioni iniziali differenti di 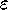 dalle precedenti,
per ottenere una differenza
accumulata crescente come
dalle precedenti,
per ottenere una differenza
accumulata crescente come 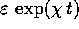 , dove
, dove 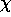 è un esponente di Lyapounov positivo.
è un esponente di Lyapounov positivo.
Possiamo concludere che un'integrazione numerica dovrebbe sempre
essere accompagnata da una stima degli esponenti di Lyapounov. Se
alcuni di questi risultano positivi, l'integrazione numerica non
potrà in nessun caso essere attendibile dopo un tempo di
propagazione pari a molte volte il tempo di Lyapounov
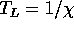 , dove
, dove 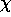 è il massimo degli esponenti di Lyapounov
(si noti che la dimensione degli esponenti di Lyapounov è
è il massimo degli esponenti di Lyapounov
(si noti che la dimensione degli esponenti di Lyapounov è
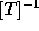 ). Per esempio, dopo un tempo
). Per esempio, dopo un tempo 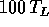 , l'effetto di ogni
piccolo errore nelle condizioni iniziali, e l'errore di troncamento
accumulato, crescono di un fattore
, l'effetto di ogni
piccolo errore nelle condizioni iniziali, e l'errore di troncamento
accumulato, crescono di un fattore 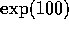 . Perciò occorre
stimare almeno il massimo degli esponenti di Lyapounov.
. Perciò occorre
stimare almeno il massimo degli esponenti di Lyapounov.
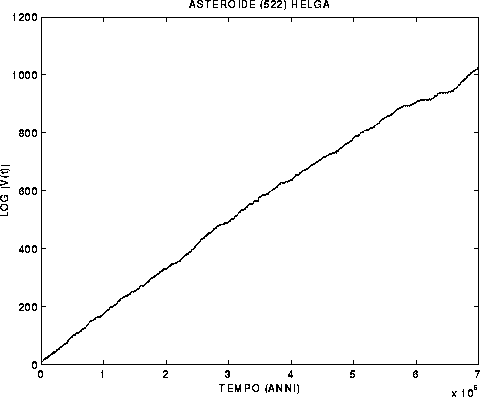
Figure 9.1: Andamento della lunghezza di un vettore
variazione, soluzione dell'equazione alle variazioni con condizione
iniziale scelta a caso, per l'asteroide (522) Helga; da
un'integrazione numerica, con un metodo di ordine molto elevato,
dell'equazione del problema dei 6 corpi (Sole, 4 pianeti,
asteroide). Il tempo di Lyapounov, in cui due orbite divergono di un
fattore exp(1), è circa 7000 anni.
In linea di principio, non è possibile calcolare esattamente il
valore del massimo esponente di Lyapounov per un'orbita di un sistema
non integrabile , perché la definizione richiede di
calcolare un limite per 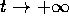 . Il metodo più semplice per
ottenere una stima temporanea del valore del massimo esponente di
Lyapounov è il seguente: si sceglie un qualunque vettore variazione
iniziale
. Il metodo più semplice per
ottenere una stima temporanea del valore del massimo esponente di
Lyapounov è il seguente: si sceglie un qualunque vettore variazione
iniziale 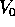 , (si può supporre
, (si può supporre 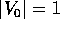 ), e si calcola la
soluzione dell'equazione alle variazioni con condizione iniziale
), e si calcola la
soluzione dell'equazione alle variazioni con condizione iniziale
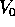 , usando lo stesso metodo di integrazione numerica usato per le
equazioni di moto. Quindi si studia l'andamento della funzione
, usando lo stesso metodo di integrazione numerica usato per le
equazioni di moto. Quindi si studia l'andamento della funzione
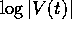 ; se esso indica un asintoto, la
pendenza dell'asintoto indica un valore stimato del massimo esponente
di Lyapounov.
; se esso indica un asintoto, la
pendenza dell'asintoto indica un valore stimato del massimo esponente
di Lyapounov.
Se viene individuato un esponente di Lyapounov positivo, non ha senso
utilizzare le specifiche predizioni contenute nella soluzione
calcolata per tempi molto più lunghi di qualche decina di tempi di
Lyapounov; non si conosce alcun metodo per formulare una predizione
attendibile, se non in senso statistico. Se al contrario la curva
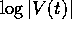 ha una pendenza che tende a zero, ha senso continuare
l'integrazione numerica, e le predizioni che essa fornisce sono
utilizzabili in senso deterministico.
ha una pendenza che tende a zero, ha senso continuare
l'integrazione numerica, e le predizioni che essa fornisce sono
utilizzabili in senso deterministico.
Come esempio di questa procedura, mostriamo nella
Figura 9.1 il caso di un asteroide, la cui
orbita mostra dipendenza critica dalle condizioni iniziali con un
esponente di Lyapounov relativamente grande (rispetto alle scale di
tempo in gioco) 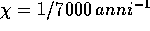 [Milani-Nobili 92].
[Milani-Nobili 92].