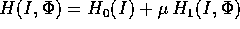 con
con 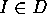 aperto di
aperto di 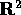 e
e 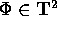 .
.
Sommario Ci limitiamo per semplicità ad enunciare e dimostrare il teorema di non integrabilità di Poincaré per una ``generica'' perturbazione di un problema integrabile a due gradi di libertà.
Teorema di non integrabilità di Poincaré :
Sia 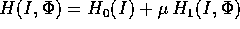 con
con 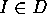 aperto di
aperto di 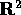 e
e 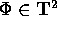 .
.
Sia la parte integrabile 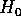 non degenere , cioè tale che
non degenere , cioè tale che
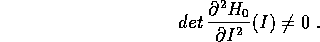
Sia la perturbazione 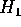 della hamiltoniana
sviluppabile in serie di Fourier uniformemente convergente:
della hamiltoniana
sviluppabile in serie di Fourier uniformemente convergente:
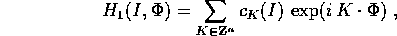
con tutti i coefficienti 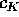 diversi da zero per
diversi da zero per 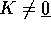 .
.
In realtà, è sufficiente che, per ogni 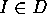 , sia
finito il numero dei coefficienti
, sia
finito il numero dei coefficienti 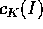 nulli.
nulli.
Allora il sistema non è integrabile, nel senso che non ha un
secondo integrale 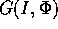 , analitico reale in
, analitico reale in  e
funzionalmente indipendente da H.
e
funzionalmente indipendente da H.
Dimostrazione:
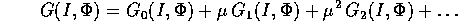
dove i puntini stanno per una serie di potenze in  ,
uniformemente convergente (in
,
uniformemente convergente (in  , con W un compatto
contenuto in D).
, con W un compatto
contenuto in D).
Se G è un integrale primo, la sua derivata totale lungo le soluzioni si annulla. Con il formalismo della parentesi di Poisson si ricava allora
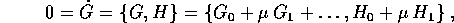
e, sviluppando in serie di potenze rispetto a  ,
,
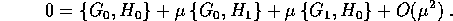
Se questa serie di potenze di  deve essere nulla identicamente
rispetto a
deve essere nulla identicamente
rispetto a  , si devono annullare i termini di ciascun ordine:
per l'ordine zero,
, si devono annullare i termini di ciascun ordine:
per l'ordine zero,

implica che 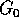 deve essere un integrale primo del sistema
integrabile con hamiltoniana
deve essere un integrale primo del sistema
integrabile con hamiltoniana 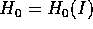 . Siano ora
. Siano ora
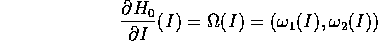
le frequenze proprie del sistema imperturbato (con hamiltoniana
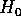 ). Tra i tori I=cost ce ne sono alcuni su cui il rapporto
delle frequenze
). Tra i tori I=cost ce ne sono alcuni su cui il rapporto
delle frequenze 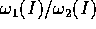 è irrazionale: per il
teorema del ritorno , in un tale toro ogni orbita di
è irrazionale: per il
teorema del ritorno , in un tale toro ogni orbita di
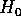 è densa e
è densa e 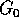 , funzione continua costante sulle
orbite, è costante. I valori di
, funzione continua costante sulle
orbite, è costante. I valori di 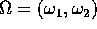 che
sono tra loro in un rapporto irrazionale sono densi nel piano delle
frequenze: inoltre l'insieme denso di frequenze con
rapporto irrazionale proviene da un insieme denso di valori di
I, dal momento che l'applicazione
che
sono tra loro in un rapporto irrazionale sono densi nel piano delle
frequenze: inoltre l'insieme denso di frequenze con
rapporto irrazionale proviene da un insieme denso di valori di
I, dal momento che l'applicazione  definita dal
gradiente di
definita dal
gradiente di 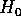 è un diffeomorfismo locale, avendo
determinante jacobiano
è un diffeomorfismo locale, avendo
determinante jacobiano
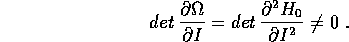
Quindi 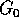 è
costante su di un insieme di tori che è denso in
è
costante su di un insieme di tori che è denso in 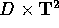 ,
e si può concludere che
,
e si può concludere che

L'equazione relativa all'ordine 1 in  è
è
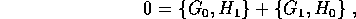
che, tenendo conto che 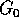 e
e 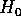 dipendono solo
dalle I, si semplifica in
dipendono solo
dalle I, si semplifica in
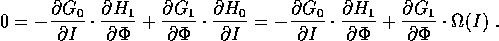
Ora, se  è un integrale primo, deve essere periodico di periodo
è un integrale primo, deve essere periodico di periodo
 nelle variabili angolo e di classe
nelle variabili angolo e di classe  , quindi ammette uno
sviluppo in serie di Fourier:
, quindi ammette uno
sviluppo in serie di Fourier:
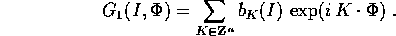
Sostituendo questo sviluppo, e quello analogo di 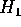 , si trova
(derivando per serie, il che è lecito perché la serie di
Fourier delle derivate è convergente):
, si trova
(derivando per serie, il che è lecito perché la serie di
Fourier delle derivate è convergente):
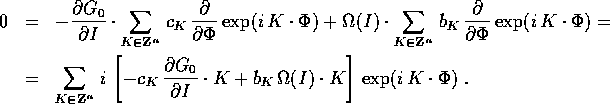
Se questa serie di Fourier deve essere identicamente nulla, tali devono essere i suoi coefficienti:
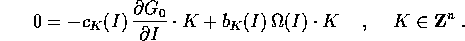
Scegliamo I in modo che il rapporto fra le frequenze
sia razionale, cioè 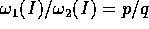 , con
, con 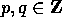 ; allora
per
; allora
per 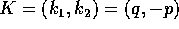 è nullo il divisore
è nullo il divisore
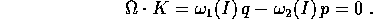
Quindi per tali valori di I e di K l'equazione nei coefficienti si riduce a
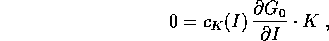
che ha due sole possibili soluzioni: o 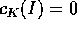 , ma questo non
è possibile (se anche
, ma questo non
è possibile (se anche 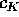 fosse nullo, non possono essere nulli
gli infiniti coefficienti
fosse nullo, non possono essere nulli
gli infiniti coefficienti 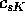 con s intero, che danno luogo
allo stesso problema); oppure
con s intero, che danno luogo
allo stesso problema); oppure

che implica che i due vettori 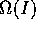 e
e 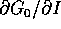 , entrambi ortogonali a K, sono paralleli: allora, poiché
, entrambi ortogonali a K, sono paralleli: allora, poiché
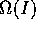 è il gradiente di
è il gradiente di 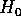 , i gradienti di
, i gradienti di 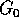 ed
ed 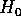 sono paralleli in I: l'insieme delle I per le quali
ciò si verifica (quelle corrispondenti ad rapporto razionale
fra le frequenze) è denso in D; perciò i due gradienti sono
sempre paralleli.
sono paralleli in I: l'insieme delle I per le quali
ciò si verifica (quelle corrispondenti ad rapporto razionale
fra le frequenze) è denso in D; perciò i due gradienti sono
sempre paralleli.
Se due funzioni hanno gradienti paralleli, sono - almeno localmente - funzionalmente dipendenti , ossia esiste una funzione F (differenziabile) tale che

Consideriamo ora la funzione
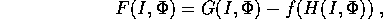
che è ancora un integrale primo e che
è identicamente nulla per 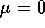 . Sviluppando di nuovo, si ha allora
. Sviluppando di nuovo, si ha allora
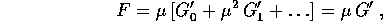
dove G' è ancora un integrale primo: ripetendo lo stesso
ragionamento, 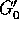 è funzionalmente dipendente da
è funzionalmente dipendente da 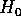 .
.
Procedendo per induzione, si dimostra che ad ogni
ordine in 
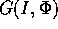 è funzionalmente dipendente da
è funzionalmente dipendente da
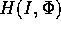 : poiché per ipotesi G è una funzione
analitica reale in
: poiché per ipotesi G è una funzione
analitica reale in  , ne segue che G=f(H) non può essere un
integrale primo indipendente dalla hamiltoniana.
, ne segue che G=f(H) non può essere un
integrale primo indipendente dalla hamiltoniana.
Per dimostrare che un dato problema non è integrabile si deve
dimostrare anche che lo
sviluppo in serie di Fourier della perturbazione 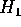 ha la
proprietà di non avere infiniti coefficienti che si annullano, o
qualche altra proprietà che può servire allo stesso scopo. Questo
fu appunto dimostrato da Poincaré per il problema dei tre
corpi; si veda [Poincaré 1892].
ha la
proprietà di non avere infiniti coefficienti che si annullano, o
qualche altra proprietà che può servire allo stesso scopo. Questo
fu appunto dimostrato da Poincaré per il problema dei tre
corpi; si veda [Poincaré 1892].
Tuttavia, alcuni anni dopo Sundman dimostrò che esiste una rappresentazione delle soluzioni del problema dei tre corpi con una serie uniformemente convergente; il premio però era già stato assegnato. Il suo risultato non contraddiceva quello di Poincaré, perché le serie di Sundman non sono del tipo utilizzato nei sistemi integrabili secondo Weierstrass. Le serie ``alla Weierstrass'' sono del tipo praticamente impiegato nelle teorie perturbative che gli astronomi utilizzano per predire le orbite dei pianeti, mentre quelle di Sundman sono difficilmente utilizzabili per calcoli di questo tipo; quindi, benché il risultato di Sundman sia di grande importanza teorica, l'impatto del teorema di non integrabilità di Poincaré sugli sviluppi della ricerca in dinamica è stato molto maggiore.