Sommario Se un campo vettoriale F è il gradiente di una funzione
-U, il sistema dinamico definito da F ammette U come funzione
di Lyapounov globale, e si possono calcolare esplicitamente tutti i
bacini di attrazione. Per i sistemi dinamici gradiente è
particolarmente semplice, nella maggior parte dei casi, discutere
l'esistenza delle soluzioni per ogni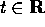 
, i punti limite e la
stabilità degli equilibri.
Definizione:
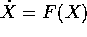definito su un aperto 
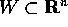tale che il campo
vettoriale F(X) è il gradiente (con segno cambiato) di una
funzione regolare U, di classe almeno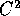 
su W:
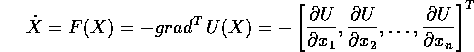
Il simbolo di trasposto è necessario perché usualmente il
gradiente è un vettore riga, mentre F(X) è un campo di
vettori colonna. Questa cautela sarà molto utile in seguito, in
particolare nel Capitolo 6. Per semplificare la
notazione, è comodo il simbolo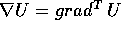 
che indica
il gradiente come vettore colonna , cioè
il vettore colonna con le derivate parziali come componenti.
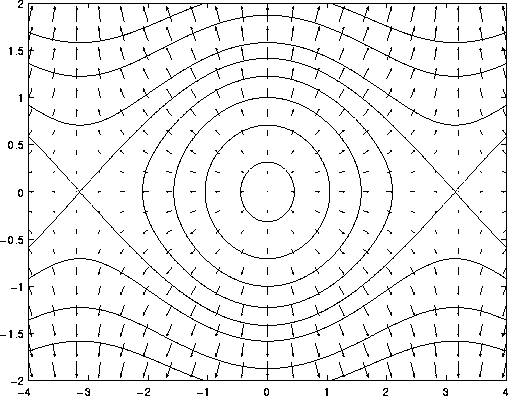
Figure 3.6: Il gradiente come campo vettoriale.
Nella figura sono disegnate sia alcune linee di livello, sia il
gradiente in un reticolo di punti.
La funzione -U(X) si indica anche con il nome di potenziale del campo vettoriale F(X); si faccia però attenzione a non confondere il potenziale dei sistemi gradienti, che è il potenziale di un campo vettoriale opposto alle velocità, con l'opposto dell'energia potenziale (per unità di massa) nei sistemi newtoniani, che è il potenziale del campo vettoriale che esprime l'accelerazione.
Il campo vettoriale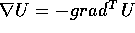 
è perpendicolare in ogni
punto alle superfici di livello U(X)=cost (per il teorema delle
funzioni implicite , e si annulla solo nei punti stazionari
della funzione U, che sono anche punti di equilibrio per il sistema
dinamico gradiente. La stabilità di questi punti di equilibrio può
essere studiata utilizzando sia il metodo della funzione di Lyapounov
che quello della linearizzazione nei punti di equilibrio.
Un sistema dinamico gradiente è dotato in modo naturale di funzioni di Lyapounov, che sono semplicemente L(X)=U(X)+const. Infatti la derivata totale
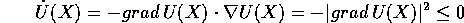
e si annulla solo nei punti di equilibrio. Perciò ogni punto S di minimo locale forte per U(X) è un punto di equilibrio asintoticamente stabile per il sistema dinamico gradiente, con funzione di Lyapounov stretta U(X)-U(S). La disponibilità di una funzione di Lyapounov ``globale'' consente di ottenere conclusioni molto precise anche sui limiti e sui bacini di attrazione:
Teorema dei punti limite di un sistema gradiente :
Sia X(t) una soluzione del sistema gradiente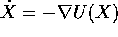 
definito sull'aperto W, tale da mantenersi per
ogni t>0 dentro un compatto K contenuto in
W. Supponiamo inoltre che i punti di equilibrio del sistema
dinamico (cioè i punti stazionari di U) siano isolati. Allora
il limite per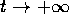 
della soluzione X(t) esiste, ed è
un punto stazionario di U(X).
Dimostrazione:
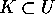, quindi si applica il teorema di
continuazione delle soluzioni . Poiché K è
compatto , ogni successione 
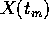con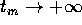 
deve avere una sottosuccessione convergente, ossia X(t) deve avere
qualche valore limite Z per 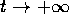. Ripetendo lo stesso
ragionamento usato nella dimostrazione del teorema di
stabilità di Lyapounov , si
ottiene che la funzione U è costante sulla soluzione passante
per Z. Ma in un sistema gradiente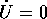 
solo nei punti di
equilibrio, quindi il valore limite Z è un equilibrio.
Resta da provare che il valore limite è un solo punto di equilibrio. Poiché i punti di equilibrio sono isolati, l'insieme dei valori limite non può contenerne più di uno per non essere sconnesso, il che contraddirebbe il teorema di invarianza degli insiemi limite .
Poiché la funzione di Lyapounov U(X)+const è globale, cioè
vale su tutto l'insieme W su cui è definito il sistema dinamico,
è possibile dare delle descrizioni globali dei bacini di attrazione
in termini dei valori di U. Supponiamo per esempio che S sia un
punto di minimo locale forte (quindi isolato) per U, e che U(S)=c sia il
valore di questo minimo: allora per ogni 
l'insieme
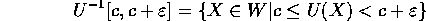
è un intorno di S, e per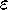 
abbastanza piccolo la sua
componente connessa Z contenente S, non conterrà altri punti
stazionari. Allora Z è positivamente invariante, ed è contenuto
nel bacino del punto asintoticamente stabile S. Per
esempio in dimensione 2, se supponiamo che tutti i punti stazionari di
U siano non degeneri (la matrice hessiana non abbia autovalore 0),
allora ci sono solo tre tipi di punto stazionario: i minimi (locali
forti), i massimi (locali forti), ed i punti di sella. Per trovare i
bacini di attrazione dei punti di minimo basta quindi tracciare le
curve di livello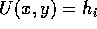 
dove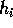 
sono i valori di U
corrispondenti ai punti di sella: gli aperti connessi delimitati da
queste curve di livello e contenenti i minimi sono contenuti nei
bacini di attrazione,
Esempio:
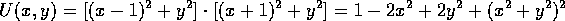
essa avrà ovviamente due minimi assoluti nei due punti stessi,
dove una delle due distanze è zero; inoltre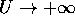 
per
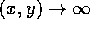. Ci sono solo tre punti stazionari,
(-1,0),(0,0),(1,0); l'origine è un punto di sella.
Il sistema dinamico gradiente che ha -U(x,y) come potenziale
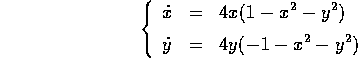
ha quindi ogni soluzione definita per ogni t>0, e con punto limite uno dei tre punti stazionari.
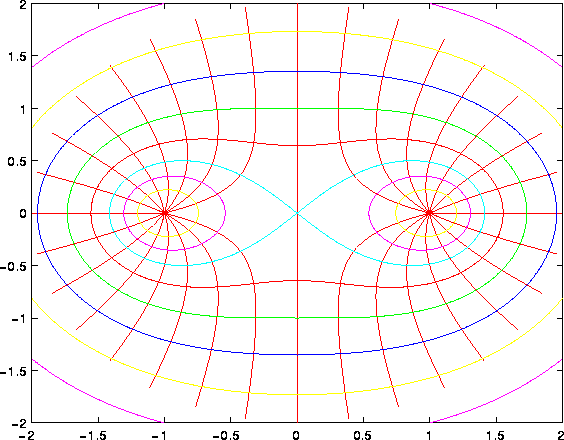
Figure 3.7: Il gradiente come sistema dinamico. Per
la funzione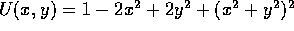 
sono disegnate sia
alcune linee di livello che alcune soluzioni del sistema dinamico
gradiente.
Problema
Nell'esempio precedente, dimostrare che le soluzioni con condizioni
iniziali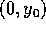 
hanno il punto di sella (0,0) come punto
limite per 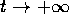, mentre tutte le soluzioni con condizioni
iniziali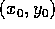 
con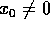 
appartengono ai bacini dei due
minimi.
Un'altra proprietà caratteristica dei sistemi dinamici gradienti è
che i sistemi linearizzati nei punti di equilibrio sono descritti da
matrici simmetriche; infatti se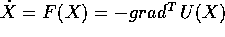 
, ed
:
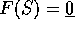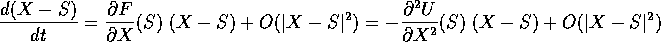
e se il campo vettoriale gradiente F(X), è di classe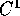 
, la
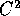funzione U è di classe e, per il teorema delle
derivate miste , le derivate seconde non
dipendono dall'ordine di
derivazione; quindi il sistema linearizzato ha come matrice meno la
matrice hessiana delle derivate seconde, che è simmetrica:
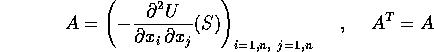
Per il teorema di diagonalizzazione delle forme quadratiche gli autovalori di una matrice simmetrica sono tutti reali, quindi coincidono con gli esponenti di Lyapounov del sistema linearizzato nel punto stazionario. Perciò si ha un pozzo dove la matrice hessiana è definita positiva (cioè quando U ha un minimo), ed una sorgente dove U ha un massimo. In tutti i casi in cui esistono autovalori con segni discordi si ha una situazione come quella della sella , cioè un punto stazionario per U che non è un estremo ha un bacino , ma non è interno al suo bacino.
Problema
Consideriamo i sistemi dinamici gradiente in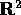 
:
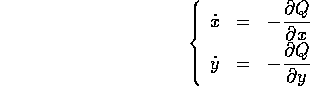
dove Q(x,y) è una forma quadratica non degenere. Dimostrare che possono avere un solo punto singolare, e che questo può essere soltanto del tipo nodo o sella, ma né centro, né fuoco, né nodo improprio.
Esercizio Studiare il sistema
