
Sommario Il moto di un corpo rigido soggetto a forze esterne (con energia potenziale data) ammette una formulazione lagrangiana e hamiltoniana, che si ricava dalla parametrizzazione del gruppo delle rotazioni con coordinate lagrangiane. Questo problema non è in generale integrabile; diventa integrabile sotto ipotesi di simmetria. Una trottola con ellissoide d'inerzia simmetrico per rotazione attorno ad un asse, sottoposta a forze esterne il cui potenziale dipenda solo dalla posizione dell'asse di simmetria, ha un moto integrabile, che può essere calcolato mediante quadrature ed inversioni.
Per poter utilizzare il formalismo lagrangiano (e hamiltoniano) nel problema del corpo rigido, occorre parametrizzare il gruppo SO(3) delle rotazioni con tre coordinate lagrangiane. Benché questo sia possibile in molti modi, il metodo classico è l'uso degli angoli di Eulero, che sono definiti a partire da una terna ortonormale di vettori nel sistema inerziale

e da una terna ortonormale di vettori nel sistema fisso con il corpo

La retta intersezione del piano (x,y) (definito da 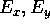 ) con il
piano
) con il
piano 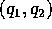 (definito da
(definito da 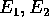 ) è la linea dei nodi .
Dei due versori diretti lungo la linea dei nodi, chiamiamo N
quello che punta verso il nodo ascendente , il cui verso è
definito dal prodotto vettore
) è la linea dei nodi .
Dei due versori diretti lungo la linea dei nodi, chiamiamo N
quello che punta verso il nodo ascendente , il cui verso è
definito dal prodotto vettore 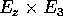 .
.
La rotazione (dipendente dal tempo) R=R(t) che manda le coordinate fisse con il corpo in quelle inerziali:

si può descrivere R come composizione di tre rotazioni (ciascuna
dipendente dal tempo). Usiamo sempre la notazione 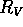 per una
rotazione attorno all'asse V di un angolo |V| (e con verso
antiorario visto dalla testa di V).
per una
rotazione attorno all'asse V di un angolo |V| (e con verso
antiorario visto dalla testa di V).
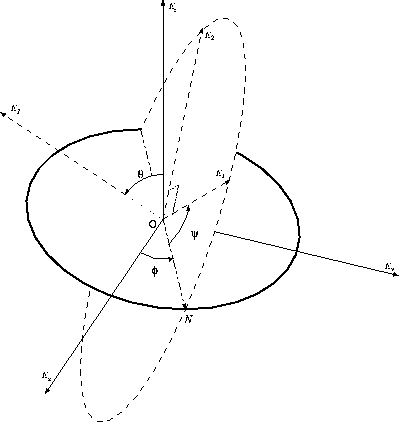
Figure 7.9: Gli angoli di Eulero di una rotazione.
 di un angolo
di un angolo 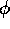 attorno all'asse
attorno all'asse 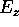 , fino a
mandare
, fino a
mandare 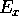 nel versore N del nodo ascendente (
nel versore N del nodo ascendente ( 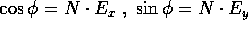 );
);
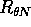 di un angolo
di un angolo  intorno all'asse N dei nodi,
fino a mandare
intorno all'asse N dei nodi,
fino a mandare 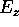 in
in 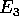 (
( 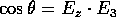 );
);
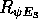 di un angolo
di un angolo 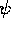 attorno all'asse
attorno all'asse 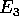 , fino a mandare
N in
, fino a mandare
N in 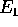 (
( 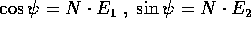 ).
).
Gli angoli di Eulero della rotazione R sono 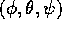 . Si noti che
. Si noti che 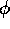 e
e 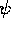 sono veramente
variabili angolo , mentre
sono veramente
variabili angolo , mentre  può
variare solo nell'intervallo
può
variare solo nell'intervallo 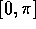 .
.
Tra gli elementi orbitali di un'orbita del problema
dei due corpi, 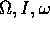 sono gli
angoli di Eulero che mandano il riferimento ortonormale dato
in una terna ortonormale con primo asse lungo il
vettore di Laplace-Lenz e terzo asse lungo il vettore
momento angolare. I non è una variabile angolo.
sono gli
angoli di Eulero che mandano il riferimento ortonormale dato
in una terna ortonormale con primo asse lungo il
vettore di Laplace-Lenz e terzo asse lungo il vettore
momento angolare. I non è una variabile angolo.
La matrice R si decompone nelle tre rotazioni
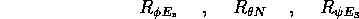
ma occorre capire in quale sequenza queste rotazioni vanno
eseguite. Teniamo presente che la matrice di rotazione delle
coordinate è l'inversa della matrice di rotazione degli assi, e che
dobbiamo passare dalle coordinate fisse nel corpo Q a quelle
inerziali X. La prima operazione da eseguire è quindi la rotazione
dell'angolo 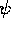 attorno a
attorno a 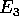 , che è l'inversa della rotazione
che manda
, che è l'inversa della rotazione
che manda 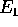 in N; poi la rotazione dell'angolo
in N; poi la rotazione dell'angolo  attorno
ad N, l'inversa della rotazione che manda
attorno
ad N, l'inversa della rotazione che manda 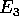 in
in 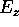 ; infine la
rotazione di
; infine la
rotazione di 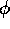 attorno ad
attorno ad 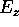 , l'inversa della rotazione che
manda N in
, l'inversa della rotazione che
manda N in 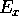 . In conclusione, eseguendo la composizione delle
rotazioni per moltiplicazione delle matrici a destra, come sempre
accade per le trasformazioni lineari:
. In conclusione, eseguendo la composizione delle
rotazioni per moltiplicazione delle matrici a destra, come sempre
accade per le trasformazioni lineari:
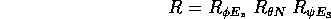
Se vogliamo scrivere esplicitamente le matrici: la rotazione 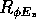 lascia fisso l'asse
lascia fisso l'asse 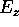 , quindi è data da
, quindi è data da
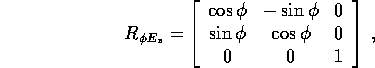
mentre la rotazione 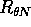 è
la rotazione attorno al primo al momento in cui viene
eseguita) asse coordinato, quindi
è
la rotazione attorno al primo al momento in cui viene
eseguita) asse coordinato, quindi
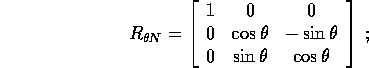
infine 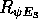 è
la rotazione attorno al terzo (al momento in cui viene eseguita) asse coordinato, quindi
è
la rotazione attorno al terzo (al momento in cui viene eseguita) asse coordinato, quindi
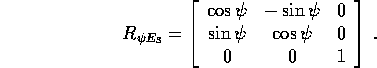
Eseguendo il prodotto di matrici si può ottenere la formula esplicita della parametrizzazione del gruppo SO(3) delle rotazioni, a cui appartiene R, con gli angoli di Eulero. Omettiamo questo calcolo perché la formula che ne risulta è complicata, e non conviene usarla direttamente.
Per poter usare il formalismo lagrangiano occorre non solo disporre
delle coordinate lagrangiane 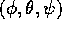 , ma anche saper
scrivere - come espressione analitica esplicita - la
lagrangiana in funzione delle sei variabili
, ma anche saper
scrivere - come espressione analitica esplicita - la
lagrangiana in funzione delle sei variabili 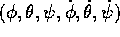 . Noi conosciamo un'espressione
dell'energia cinetica in funzione di
. Noi conosciamo un'espressione
dell'energia cinetica in funzione di 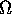 , il vettore velocità
angolare in coordinate fisse con il corpo: occorre trovare le formule
analitiche che legano queste variabili.
, il vettore velocità
angolare in coordinate fisse con il corpo: occorre trovare le formule
analitiche che legano queste variabili.
Teorema della lagrangiana del corpo rigido :
Se un corpo rigido ruota con velocità angolare
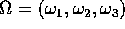 (nelle coordinate fisse con il
corpo) fra
(nelle coordinate fisse con il
corpo) fra 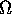 e gli angoli di Eulero
e gli angoli di Eulero 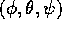 ,
intercorre la relazione
,
intercorre la relazione
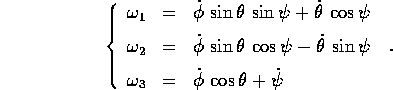
Dimostrazione:
Per la regola della velocità angolare , nel caso in cui non ci sia moto di traslazione si ha
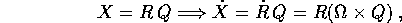
da cui si ricava
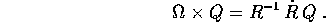
Allora  è il vettore assiale associato
alla matrice antisimmetrica
è il vettore assiale associato
alla matrice antisimmetrica 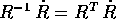 .
Per calcolare quest'ultima, osserviamo che
.
Per calcolare quest'ultima, osserviamo che
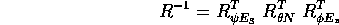
e calcoliamo - con la regola di Leibnitz per le matrici - la derivata del prodotto:
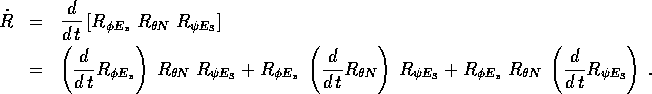
Moltiplichiamo tra loro le ultime due formule, semplificando:
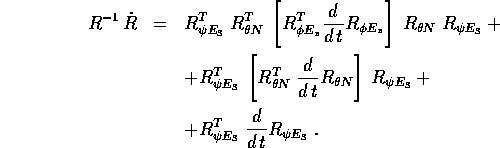
Cominciamo il ragionamento con il termine più semplice, che è
l'ultimo. Per il teorema delle rotazioni infinitesimali ,
ogni matrice di rotazione è esprimibile come esponenziale di una
matrice antisimmetrica; nel caso di una rotazione attorno ad uno degli
assi coordinati come per 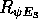 , è facile trovare la matrice
antisimmetrica:
, è facile trovare la matrice
antisimmetrica:
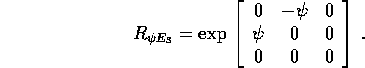
Allora, per il teorema di derivazione dell'esponenziale ,
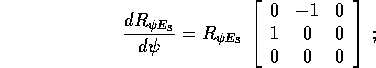
la derivata rispetto a t si ottiene da questa formula semplicemente
moltiplicando per 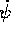 . In conclusione, il terzo termine di
. In conclusione, il terzo termine di
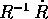 è
è
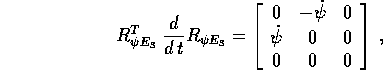
ed il corrispondente contributo al vettore  è
è 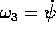 .
In modo del tutto analogo
.
In modo del tutto analogo
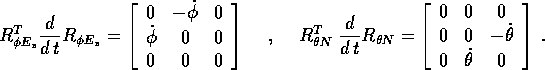
Però i contributi di questi due termini ad 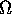 sono un po'
più complicati, perché in
sono un po'
più complicati, perché in 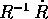 appaiono coniugati con
rotazioni. Anche se si potrebbero eseguire le 6 moltiplicazioni
di matrice richieste, è conveniente sfruttare a fondo
l'identificazione tra matrice antisimmetrica
appaiono coniugati con
rotazioni. Anche se si potrebbero eseguire le 6 moltiplicazioni
di matrice richieste, è conveniente sfruttare a fondo
l'identificazione tra matrice antisimmetrica 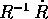 e
vettore assiale
e
vettore assiale 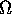 .
.
Lemma:
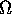 è il vettore assiale della matrice antisimmetrica S,
cioè se per ogni vettore
è il vettore assiale della matrice antisimmetrica S,
cioè se per ogni vettore 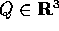

allora, per ogni rotazione 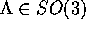 ,
, 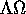 è il
vettore assiale della matrice
è il
vettore assiale della matrice 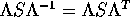 coniugata di S tramite
coniugata di S tramite 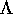 :
:
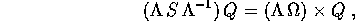
Dimostrazione del lemma:
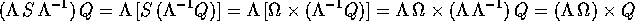
Il lemma asserisce che il vettore assiale (ottenuto da una matrice antisimmetrica disponendo i coefficienti non nulli della matrice in un certo ordine) si trasforma come un vettore ``normale'' per effetto di un cambiamento ortogonale di sistema di coordinate cartesiane.
Ora possiamo trasformare la formula per la matrice antisimmetrica
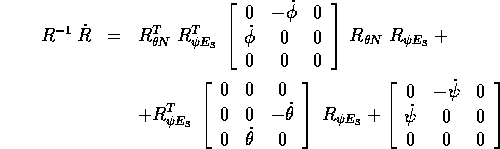
nella formula per il vettore assiale corrispondente 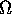 :
:
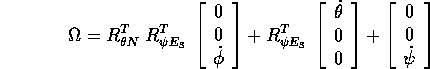
e calcolando si ottiene la tesi:
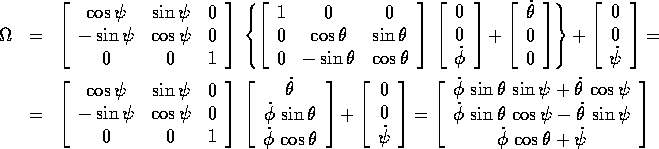
Grazie al teorema appena dimostrato, possiamo esprimere in funzione
degli angoli di Eulero e delle loro derivate la velocità angolare e
quindi l'energia cinetica (rispetto al centro di massa, o con centro
di massa fisso) 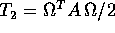 . Supponendo che
. Supponendo che
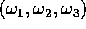 siano le coordinate rispetto agli
assi d'inerzia (che significa che la terna
siano le coordinate rispetto agli
assi d'inerzia (che significa che la terna 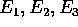 è
formata dai versori degli assi d'inerzia), si ha
è
formata dai versori degli assi d'inerzia), si ha
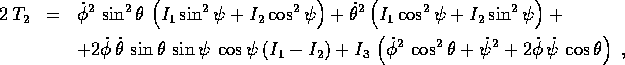
dove 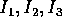 sono i momenti principali d'inerzia. Se il moto
è libero, oppure se le forze esterne ammettono un'energia potenziale
sono i momenti principali d'inerzia. Se il moto
è libero, oppure se le forze esterne ammettono un'energia potenziale
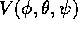 , questo consente di scrivere la
lagrangiana del moto di rotazione (riferito al centro di
massa, o con centro di massa fisso) come
, questo consente di scrivere la
lagrangiana del moto di rotazione (riferito al centro di
massa, o con centro di massa fisso) come
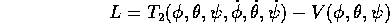
e di ricavare le equazioni di Lagrange (oppure, previa trasformata di Legendre , le equazioni di Hamilton ).
Possiamo ora completare la dimostrazione del teorema del momento angolare , utilizzando gli angoli di Eulero come parametrizzazione esplicita dello spazio delle configurazioni SO(3) del corpo rigido con centro di massa fisso. Si noti che l'argomentazione che segue si applica indifferentemente al caso del corpo rigido discreto o continuo.
L'angolo 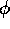 , variabile ciclica per la lagrangiana
, variabile ciclica per la lagrangiana 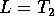 , fornisce
infatti un integrale primo dato da
, fornisce
infatti un integrale primo dato da
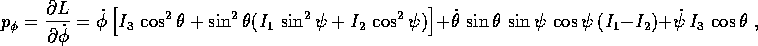
che coincide con la proiezione lungo 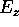 del momento angolare C del
corpo, come si verifica calcolando
del momento angolare C del
corpo, come si verifica calcolando
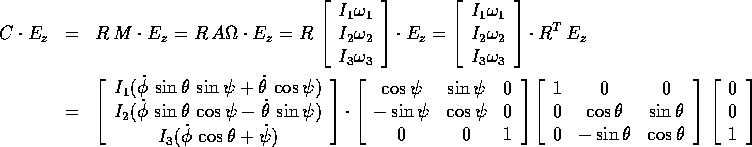
dove si è tenuto conto che
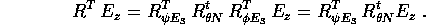
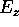 può essere scelto arbitrariamente nel riferimento inerziale
per definire gli angoli di Eulero; per ogni scelta,
può essere scelto arbitrariamente nel riferimento inerziale
per definire gli angoli di Eulero; per ogni scelta, 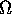 non
dipende da
non
dipende da 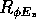 , quindi
, quindi 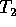 non dipende da
non dipende da 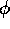 ; si
ricava che è costante la componente di C rispetto a un asse
qualsiasi, cioè che C è un vettore di integrali primi.
; si
ricava che è costante la componente di C rispetto a un asse
qualsiasi, cioè che C è un vettore di integrali primi.
La lagrangiana del moto di rotazione del corpo rigido è abbastanza complicata, avendo tre gradi di libertà; in generale darà luogo ad un problema non integrabile . Ci sono però dei casi particolari integrabili , tra cui abbiamo già trattato il caso libero, ossia con energia potenziale nulla.
Un altro caso integrabile è quello del rotore simmetrico ,
ossia con ellissoide d'inerzia biassiale e con potenziale dipendente
solo dall'angolo di Eulero  ; in tal caso
; in tal caso 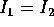 , e la
formula dell'energia cinetica si semplifica molto:
, e la
formula dell'energia cinetica si semplifica molto:
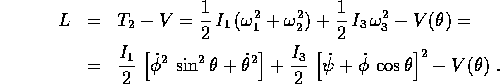
Ci sono due variabili cicliche
 , e i corrispondenti momenti
, e i corrispondenti momenti
 sono integrali primi:
sono integrali primi:
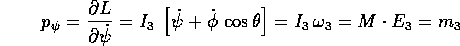
è la componente del momento angolare (rispetto al centro di massa) 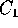 lungo l'asse di simmetria dell'ellissoide d'inerzia, mentre
lungo l'asse di simmetria dell'ellissoide d'inerzia, mentre
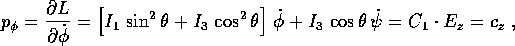
come già visto, è la componente di 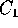 lungo l'asse
lungo l'asse
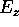 . Inoltre abbiamo l'integrale dell'energia
. Inoltre abbiamo l'integrale dell'energia 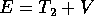 , perciò il
sistema è integrabile.
, perciò il
sistema è integrabile.
Eseguiamo la trasformata di Legendre , usando la formula della matrice inversa per trasformare la forma quadratica nelle velocità in quella nei momenti:
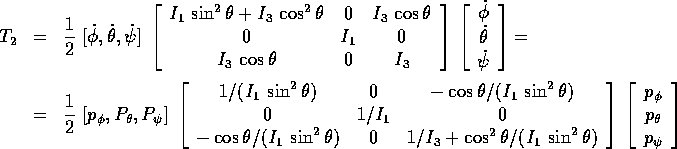
da cui si deduce la formula della hamiltoniana
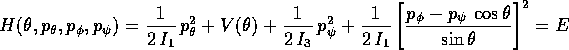
che può essere interpretata come hamiltoniana ad un grado di
libertà, con coordinata  , momento
, momento
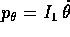 , e due parametri costanti:
, e due parametri costanti:
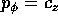 e
e 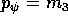 . Quindi il problema non solo è
integrabile, ma può essere integrato usando soltanto
operazioni di quadratura , come descritto nella
Sezione 5.2.
. Quindi il problema non solo è
integrabile, ma può essere integrato usando soltanto
operazioni di quadratura , come descritto nella
Sezione 5.2.
Esercizio Svolgere tutti i passaggi della trasformazione di Legendre qua sopra.
Esercizio
Verificare che i tre integrali primi 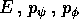 sono
in commutazione , e che hanno gradienti linearmente
indipendenti, salvo se l'asse
sono
in commutazione , e che hanno gradienti linearmente
indipendenti, salvo se l'asse 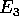 è esattamente lungo
è esattamente lungo
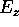 .
.
L'ipotesi 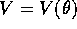 equivale ad affermare che le forze esterne che
hanno effetto sulla rotazione del corpo rigido dipendono solo
dall'inclinazione
equivale ad affermare che le forze esterne che
hanno effetto sulla rotazione del corpo rigido dipendono solo
dall'inclinazione  . Per esempio questo si verifica se il corpo
ha simmetria assiale , cioè densità che non dipende da
. Per esempio questo si verifica se il corpo
ha simmetria assiale , cioè densità che non dipende da
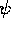 , ed è soggetto ad un campo gravitazionale con potenziale
dipendente soltanto di z.
, ed è soggetto ad un campo gravitazionale con potenziale
dipendente soltanto di z.
Per esempio se supponiamo che l'energia potenziale sia della forma

con K>0, abbiamo il sistema ad un grado di libertà con hamiltoniana
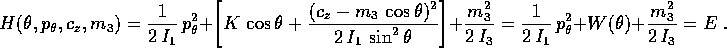
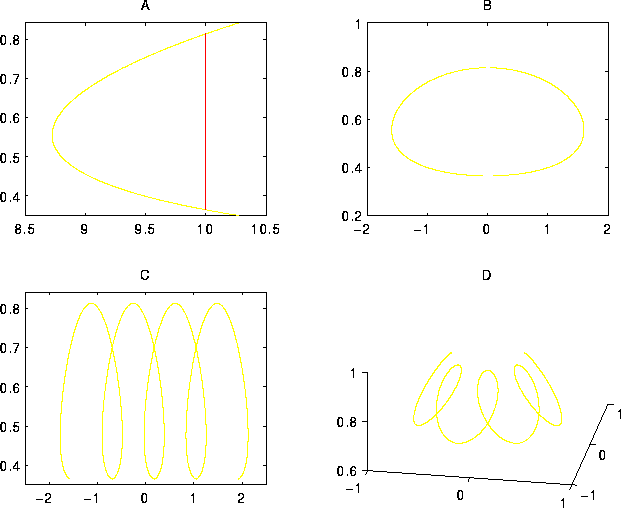
Figure: Soluzione del problema del rotore
simmetrico: (a) potenziale effettivo W (b) curva di livello
dell'energia nel problema ridotto ad un grado di libertà
(c) soluzione nel piano dei primi due angoli di Eulero
(d) intersezione dell'asse di rotazione con una sfera.
Trascuriamo il termine costante 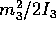 , ponendo
, ponendo 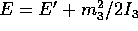 .
Lo studio qualitativo delle soluzioni, per un dato valore degli integrali
.
Lo studio qualitativo delle soluzioni, per un dato valore degli integrali
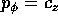 e
e 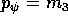 , si ottiene come al solito studiando
la funzione energia potenziale effettiva
, si ottiene come al solito studiando
la funzione energia potenziale effettiva
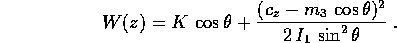
Lo studio qualitativo è molto semplice, poiché in ogni caso (tranne
che per 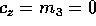 )
)
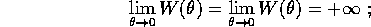
quindi
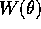 ha un minimo
ha un minimo 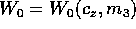 . Si può
verificare che l'insieme dei
. Si può
verificare che l'insieme dei  per cui
per cui 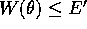 è sempre un intervallo
per ogni
è sempre un intervallo
per ogni 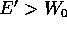 : ponendo
: ponendo 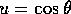 , si ha
, si ha
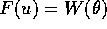
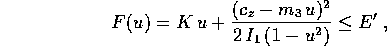
che è verificata se e solo se (moltiplicando per il denominatore che è >0)
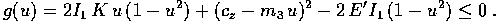
Il polinomio di terzo grado g(u) ha coefficiente di grado
massimo <0, e inoltre 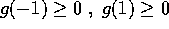 ;
deve perciò avere una radice >1, ed al più altre due
radici reali, che sono entrambe interne o entrambe esterne
all'intervallo [-1,1]: la diseguaglianza
;
deve perciò avere una radice >1, ed al più altre due
radici reali, che sono entrambe interne o entrambe esterne
all'intervallo [-1,1]: la diseguaglianza 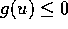 sarà soddisfatta
sull'intervallo limitato da queste due radici.
sarà soddisfatta
sull'intervallo limitato da queste due radici.
Problema
Discutere i casi 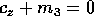 e
e 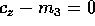 in cui lo studio
qualitativo ha un caso eccezionale.
in cui lo studio
qualitativo ha un caso eccezionale.
Suggerimento: Tenere conto del fatto che per 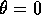 e per
e per
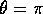 gli angoli di Eulero non sono coordinate
lagrangiane (le rotazioni
gli angoli di Eulero non sono coordinate
lagrangiane (le rotazioni 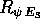 ed
ed 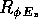 non sono distinte, quindi le due variabili
non sono distinte, quindi le due variabili 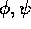 hanno
gradienti linearmente dipendenti).
hanno
gradienti linearmente dipendenti).
Figure 7.11: Rotore simmetrico: la curva tracciata sulla
sfera unitaria dal versore dell'asse di simmetria dell'ellissoide
d'inerzia assume aspetti diversi a seconda del valore degli integrali
primi; passando da a,b,c,d il valore degli integrali primi del
momento angolare resta lo stesso, mentre l'energia diminuisce.
Le soluzioni del problema del rotore simmetrico, ottenute per
quadratura , possono perciò essere descritte come segue (vedi
figura 7.10). La variabile  oscillerà
tra un valore minimo
oscillerà
tra un valore minimo  ed un valore massimo
ed un valore massimo
 (corrispondenti alle due radici
(corrispondenti alle due radici 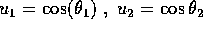 del polinomio g(u)).
L'inversa della legge oraria
del polinomio g(u)).
L'inversa della legge oraria 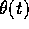 si ottiene dalla quadratura
si ottiene dalla quadratura
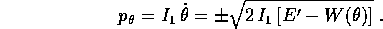
Nota la soluzione 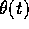 , la soluzione
, la soluzione 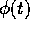 si
ricava da un'altra quadratura: ottenendo
si
ricava da un'altra quadratura: ottenendo 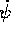 dagli
integrali primi
dagli
integrali primi 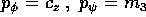 si ha
si ha
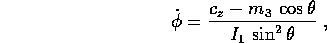
e sostituendo nell'integrale 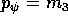 si giunge alla
quadratura che dà
si giunge alla
quadratura che dà  :
:
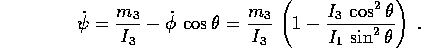
Una soluzione dotata di proprietà particolari è quella che
corrisponde al punto di minimo 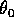 di
di 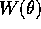 ,
cioè
,
cioè 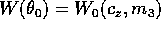 . Allora il valore di
. Allora il valore di
 resta costante, e così pure la frequenza di
precessione
resta costante, e così pure la frequenza di
precessione 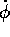 e la velocità angolare di rotazione
attorno all'asse di simmetria
e la velocità angolare di rotazione
attorno all'asse di simmetria 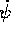 . Per valori di E'
appena superiori a
. Per valori di E'
appena superiori a 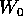 si hanno delle piccole oscillazioni
di
si hanno delle piccole oscillazioni
di  attorno al valore
attorno al valore 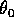 , e quindi anche il
valore di
, e quindi anche il
valore di 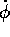 e quello di
e quello di 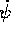 oscillano attorno
ad un valore medio. Se si traccia la figura descritta
dal vettore
oscillano attorno
ad un valore medio. Se si traccia la figura descritta
dal vettore 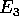 sulla sfera unitaria, queste oscillazioni
sovrapposte al moto di precessione media formano dei riccioli
(Figura 7.11).
sulla sfera unitaria, queste oscillazioni
sovrapposte al moto di precessione media formano dei riccioli
(Figura 7.11).
Un problema di moto del corpo rigido che è stato studiato intensamente, anche perché si presta ad una efficace verifica sperimentale, è quello della trottola pesante . Per trottola si intende un rotore simmetrico, vincolato ad avere un punto fisso situato sull'asse di simmetria; questo punto però non coincide con il centro di massa, per cui il peso del corpo rigido produce una coppia rispetto al punto di appoggio.
Intuitivamente, il punto fisso è un estremo di un asta, coincidente con l'asse di simmetria, appoggiato su di un piano in modo da consentire i movimenti di rotazione attorno ad esso. Negli esperimenti pratici con le trottole, è bene tenere conto del fatto che un appoggio senza attrito è un'astrazione matematica; in pratica la trottola avrà dei movimenti irregolari di traslazione dovuti anche all'attrito fra il piano e l'asse di rotazione nel punto di appoggio: in questo consiste il gioco della trottola, che non si sa mai dove va a finire. Se però si osserva soltanto il moto rispetto al punto di appoggio, il modello matematico qui presentato risulta notevolmente aderente alla realtà del semplice esperimento fisico.
Per formalizzare il problema occorre ricalcolare l'energia
cinetica del corpo rigido W con densità 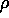 , assumendo
che il punto fisso non sia il centro di massa, ma sia
l'origine delle coordinate fisse con il corpo Q, e delle
coordinate inerziali X. Allora la velocità dovuta alla
sola rotazione sarà
, assumendo
che il punto fisso non sia il centro di massa, ma sia
l'origine delle coordinate fisse con il corpo Q, e delle
coordinate inerziali X. Allora la velocità dovuta alla
sola rotazione sarà

e l'energia cinetica, grazie all'assenza del termine di traslazione, sarà data da
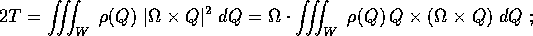
in altre parole, l'energia cinetica potrà sempre essere
definita come forma quadratica nella velocità angolare
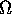 , mediante un tensore d'inerzia I.
Tuttavia il tensore d'inerzia rispetto al punto d'appoggio non
è il tensore d'inerzia rispetto al centro di massa.
, mediante un tensore d'inerzia I.
Tuttavia il tensore d'inerzia rispetto al punto d'appoggio non
è il tensore d'inerzia rispetto al centro di massa.
Teorema di Steiner :
Fra il tensore d'inerzia A rispetto al centro di massa 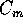 ed
il tensore d'inerzia B rispetto ad un punto qualsiasi
ed
il tensore d'inerzia B rispetto ad un punto qualsiasi
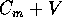 intercorre la relazione
intercorre la relazione
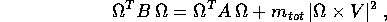
Dimostrazione:
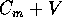 , e Z
sono le coordinate con origine nel centro di massa, allora
Q=Z-V. Consideriamo l'espressione che appare nella
definizione dell'energia cinetica, e quindi del tensore
d'inerzia:
, e Z
sono le coordinate con origine nel centro di massa, allora
Q=Z-V. Consideriamo l'espressione che appare nella
definizione dell'energia cinetica, e quindi del tensore
d'inerzia:
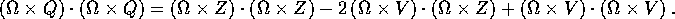
Allora l'energia cinetica è
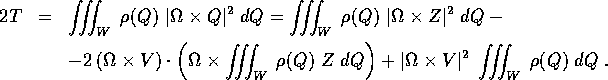
In questa formula il secondo integrale concide con quello del centro di massa:
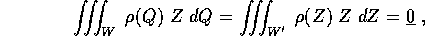
dove W' è W nel riferimento delle coordinate Z.
Il terzo integrale è quello della massa totale 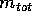 , quindi
l' energia cinetica si riduce a
, quindi
l' energia cinetica si riduce a
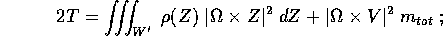
per la definizione del tensore d'inerzia, la tesi è dimostrata.
Perciò per la trottola, il momento d'inerzia rispetto al
punto di appoggio, che per ipotesi sta sull'asse d'inerzia
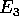 con momento principale d'inerzia
con momento principale d'inerzia 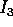 , ha momenti
principali
, ha momenti
principali 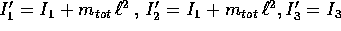 , dove
, dove 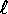 è la distanza del centro di massa dal
punto di appoggio. A parte la sostituzione dei momenti
d'inerzia modificati, la lagrangiana della trottola è
identica a quella del rotore simmetrico, quindi la soluzione
è quella già descritta precedentemente.
è la distanza del centro di massa dal
punto di appoggio. A parte la sostituzione dei momenti
d'inerzia modificati, la lagrangiana della trottola è
identica a quella del rotore simmetrico, quindi la soluzione
è quella già descritta precedentemente.