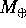 e di raggio
e di raggio 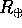 . La principale ipotesi
semplificatrice è che l'energia potenziale gravitazionale del
pianeta sia funzione solo della distanza r dal centro di massa del
pianeta, ed esattamente
. La principale ipotesi
semplificatrice è che l'energia potenziale gravitazionale del
pianeta sia funzione solo della distanza r dal centro di massa del
pianeta, ed esattamente
Sommario In molti casi, una missione spaziale può essere descritta con buona approssimazione come problema dei due corpi, dal quale perciò si possono dedurre le leggi fondamentali dell'astronautica. Per i tipi più semplici e importanti di missioni presentiamo, per lo più sotto forma di problemi proposti, il calcolo approssimato delle orbite, delle condizioni di lancio e delle manovre con razzi.
Supponiamo di studiare l'orbita di un veicolo spaziale nel campo
gravitazionale di un pianeta, per esempio la Terra, di massa
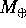 e di raggio
e di raggio 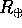 . La principale ipotesi
semplificatrice è che l'energia potenziale gravitazionale del
pianeta sia funzione solo della distanza r dal centro di massa del
pianeta, ed esattamente
. La principale ipotesi
semplificatrice è che l'energia potenziale gravitazionale del
pianeta sia funzione solo della distanza r dal centro di massa del
pianeta, ed esattamente
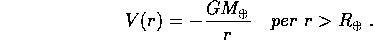
La legittimità di questa approssimazione deriva dal teorema di Newton, per cui un corpo con simmetria sferica (nel senso che la densità dipende solo da r) genera al di fuori del corpo stesso un campo gravitazionale identico a quello generato da un corpo puntiforme della stessa massa posto nel suo centro. Questo teorema è conseguenza diretta della formula di Gauss , che applicata al campo gravitazionale (solenoidale fuori dai corpi) fornisce la formula che serve a determinare la massa M di un pianeta: se S è una superficie chiusa che racchiude all'interno il pianeta (con versore normale esterno N) e F è il suo campo gravitazionale,
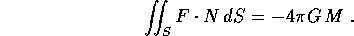
Se il pianeta ha simmetria sferica, allora il campo di forze è centrale; quando S è la sfera r=cost si ha
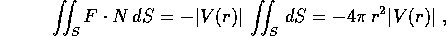
ed eguagliando le due espressioni

Perciò l'approssimazione che useremo consiste nel supporre un pianeta non puntiforme, ma con perfetta simmetria sferica.
Definizione:
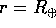 , la prima velocità cosmica
, la prima velocità cosmica 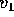 è la minima velocità di un'orbita posta appena sopra la
superficie del pianeta, cioè la velocità di un'orbita circolare
con semiasse
è la minima velocità di un'orbita posta appena sopra la
superficie del pianeta, cioè la velocità di un'orbita circolare
con semiasse 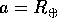 . Per la terza legge di Keplero
. Per la terza legge di Keplero
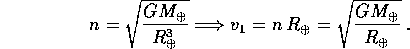
Poiché in questa definizione si trascura sia la topografia del pianeta che l'eventuale atmosfera, la prima velocità cosmica non ha alcun significato realistico nel progetto del lancio di un satellite artificiale, come si vedrà nel problema successivo.
La seconda velocità cosmica ,
detta anche velocità di fuga 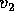 ,
è la minima velocità da imprimere ad un veicolo spaziale che parte
da
,
è la minima velocità da imprimere ad un veicolo spaziale che parte
da 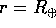 per sfuggire al campo gravitazionale del pianeta
(ovvero per porsi su un'orbita illimitata, con energia E=0). Per la formula dell'energia:
per sfuggire al campo gravitazionale del pianeta
(ovvero per porsi su un'orbita illimitata, con energia E=0). Per la formula dell'energia:
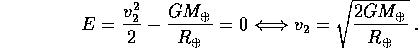
La velocità di fuga non dipende dalla direzione di lancio, che
può avvenire in qualsiasi direzione sopra al piano tangente, ed è
maggiore di un fattore 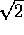 della prima velocità
cosmica. Perciò i satelliti artificiali richiedono velocità di
lancio che stanno in un intervallo relativamente ristretto.
della prima velocità
cosmica. Perciò i satelliti artificiali richiedono velocità di
lancio che stanno in un intervallo relativamente ristretto.
Problema
Cerchiamo di calcolare le velocità richieste per una procedura di
lancio di un satellite artificiale che sia abbastanza
realistica. Si vuole ottenere un'orbita circolare ad un altezza h
rispetto alla superficie del pianeta 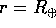 . Procediamo per
passi:
. Procediamo per
passi:
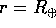 ed
apogeo (cioè l'apocentro) ad
ed
apogeo (cioè l'apocentro) ad 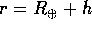 .
.
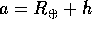 .
In questo caso la direzione è ovvia, in quanto l'incremento di velocità
deve essere parallelo alla velocità stessa all'apogeo (elevazione ù
nulla). Calcoliamo il periodo di tale orbita circolare.
.
In questo caso la direzione è ovvia, in quanto l'incremento di velocità
deve essere parallelo alla velocità stessa all'apogeo (elevazione ù
nulla). Calcoliamo il periodo di tale orbita circolare.
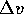 necessario per questa missione, e confrontiamolo con la prima
velocità cosmica.
necessario per questa missione, e confrontiamolo con la prima
velocità cosmica.
 , calcoliamo quale risparmio nel
, calcoliamo quale risparmio nel 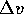 totale è possibile se si lancia dall'equatore ``verso est'',
cioè sfruttando la velocità di rotazione della piattaforma di
lancio.
totale è possibile se si lancia dall'equatore ``verso est'',
cioè sfruttando la velocità di rotazione della piattaforma di
lancio.
Resta da spiegare perché si è scelto, nel problema
precedente, un lancio in cui è nulla l'elevazione (angolo rispetto all'orizzonte,
cioè al piano tangente), in modo da avere il perigeo
alla superficie del pianeta 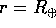 . Un lancio con elevazione
. Un lancio con elevazione
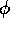 positiva immetterebbe il veicolo spaziale su un'orbita di
trasferimento con perigeo più basso di
positiva immetterebbe il veicolo spaziale su un'orbita di
trasferimento con perigeo più basso di 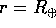 e quindi con
minore energia; però aumenterebbe l'energia richiesta dalla manovra
di circolarizzazione dell'orbita. Si tratta di vedere quale è la
scelta ottimale, che minimizza l'incremento di velocità totale
e quindi con
minore energia; però aumenterebbe l'energia richiesta dalla manovra
di circolarizzazione dell'orbita. Si tratta di vedere quale è la
scelta ottimale, che minimizza l'incremento di velocità totale
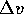 .
.
Teorema di Hohmann :
Sia data una piattaforma di lancio in moto circolare uniforme, con
velocità angolare  , a distanza R dal centro di un
pianeta con simmetria sferica di massa M; supponiamo inoltre che
, a distanza R dal centro di un
pianeta con simmetria sferica di massa M; supponiamo inoltre che
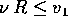 . Per lanciare un satellite del pianeta in un'orbita
circolare di raggio R+h (h>0) con due cambiamenti di velocità
impulsivi (istantanei), l'orbita di trasferimento che
minimizza l'incremento di velocità totale
. Per lanciare un satellite del pianeta in un'orbita
circolare di raggio R+h (h>0) con due cambiamenti di velocità
impulsivi (istantanei), l'orbita di trasferimento che
minimizza l'incremento di velocità totale 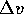 è quella che ha pericentro in
r=R, apocentro in r=R+h, piano orbitale coincidente con
quello del moto della piattaforma e verso concorde.
è quella che ha pericentro in
r=R, apocentro in r=R+h, piano orbitale coincidente con
quello del moto della piattaforma e verso concorde.
Questo teorema è la generalizzazione di un risultato pubblicato da un pioniere dell'astronautica, W. Hohmann, nel 1925. L'orbita ellittica tangente alle due circonferenze, come descritto dal teorema, si chiama orbita di trasferimento di Hohmann .
Il teorema di Hohmann si può usare in due casi. Nel primo, la
piattaforma di lancio può essere sull'equatore del pianeta che ruota
con velocità angolare  , e quindi il teorema di Hohmann tiene
conto anche del contributo dato dalla rotazione del pianeta; in questo
caso
, e quindi il teorema di Hohmann tiene
conto anche del contributo dato dalla rotazione del pianeta; in questo
caso 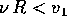 , altrimenti il veicolo spaziale non sarebbe
attaccato al suolo prima del lancio (ed il pianeta non
potrebbe restare in un solo pezzo). Nel secondo caso la ``piattaforma
di lancio'' può essere il veicolo spaziale stesso, già in
un'orbita circolare di raggio R e moto medio
, altrimenti il veicolo spaziale non sarebbe
attaccato al suolo prima del lancio (ed il pianeta non
potrebbe restare in un solo pezzo). Nel secondo caso la ``piattaforma
di lancio'' può essere il veicolo spaziale stesso, già in
un'orbita circolare di raggio R e moto medio 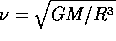 :
quindi
:
quindi 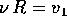 , e il teorema descrive l'orbita di trasferimento
ottimale tra due orbite circolari concentriche e coplanari.
, e il teorema descrive l'orbita di trasferimento
ottimale tra due orbite circolari concentriche e coplanari.
Dimostrazione:
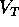 la velocità della piattaforma di lancio e
la velocità della piattaforma di lancio e 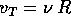 il suo modulo,
il suo modulo, 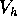 con modulo
con modulo 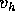 la velocità d'arrivo all'altezza
desiderata r=R+h,
la velocità d'arrivo all'altezza
desiderata r=R+h, 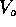 la velocità dell'orbita circolare finale
con modulo
la velocità dell'orbita circolare finale
con modulo 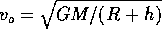 , e infine
, e infine 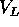 la velocità di
lancio con modulo
la velocità di
lancio con modulo 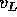 . La quantità da minimizzare è la somma dei
moduli dei due cambiamenti di velocità, cioè
. La quantità da minimizzare è la somma dei
moduli dei due cambiamenti di velocità, cioè
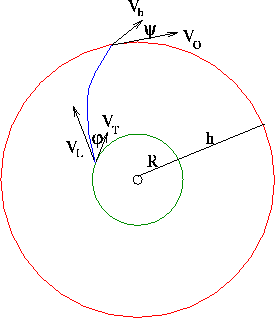
Figure 7.5: Dimostrazione del teorema di Hohmann:
definizione delle velocità della piattaforma, di lancio, di arrivo
all'altezza di destinazione, ed orbitale; angoli di elevazione al
lancio ed all'altezza di destinazione.
Per semplificare questa espressione, disponiamo dei due integrali primi E,c che devono avere lo stesso valore immediatamente dopo il lancio ad r=R ed all'arrivo ad r=R+h. Usando l'energia, si ha
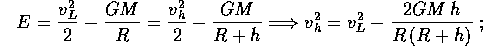
usando il momento angolare, se 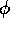 è l'elevazione ad r=R e
è l'elevazione ad r=R e 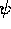 è l'elevazione ad r=R+h, si ricava
è l'elevazione ad r=R+h, si ricava
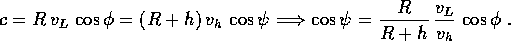
Calcoliamo gli incrementi di velocità: al lancio
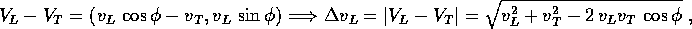
mentre all'arrivo ad r=R+h l'incremento di velocità si semplifica usando le formule ricavate dagli integrali primi:
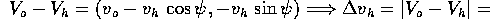
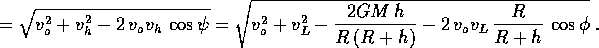
In conclusione, se poniamo 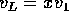 (x è la velocità di lancio
riscalata), il rapporto fra l'incremento di velocità totale e la
prima velocità cosmica
(x è la velocità di lancio
riscalata), il rapporto fra l'incremento di velocità totale e la
prima velocità cosmica 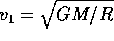 è
è
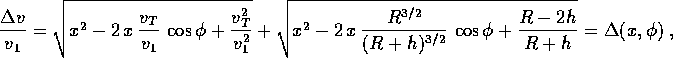
funzione delle due variabili x
e 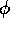 (elevazione al lancio). Si tratta di
trovare il minimo di questa funzione di due variabili, tenendo conto
del vincolo per cui l'orbita di trasferimento deve avere distanza
all'apocentro
(elevazione al lancio). Si tratta di
trovare il minimo di questa funzione di due variabili, tenendo conto
del vincolo per cui l'orbita di trasferimento deve avere distanza
all'apocentro 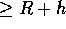 perché l'immissione nell'orbita circolare di
destinazione sia possibile. La derivata rispetto a
perché l'immissione nell'orbita circolare di
destinazione sia possibile. La derivata rispetto a 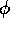 ,
,
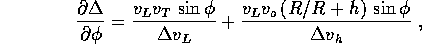
permette di osservare che il minimo rispetto a 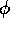 si verifica per
si verifica per 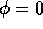 qualunque
sia
qualunque
sia 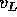 . Quindi l'orbita di trasferimento deve avere il pericentro in r=R.
Per trovare la velocità di lancio
. Quindi l'orbita di trasferimento deve avere il pericentro in r=R.
Per trovare la velocità di lancio 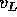 si può derivare rispetto ad x
per
si può derivare rispetto ad x
per  :
:
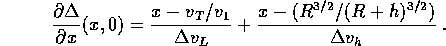
Poiché x>1 (altrimenti l'orbita di trasferimento avrebbe
l'apocentro in r=R e non arriverebbe mai ad r=R+h) la derivata
parziale rispetto ad x è sempre positiva, quindi il minimo si ha
per il minimo valore di 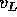 che consenta di arrivare
ad r=R+h: questo valore è calcolato nel Problema precedente.
che consenta di arrivare
ad r=R+h: questo valore è calcolato nel Problema precedente.
Poiché tutti questi calcoli sono stati eseguiti supponendo che la
traiettoria della piattaforma di lancio, l'orbita di trasferimento e
l'orbita di destinazione appartengano allo stesso piano, resta da dimostrare
che non c'è una traiettoria più efficiente fuori dal piano: ma le
componenti fuori dal piano di 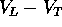 e di
e di 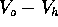 aumentano il
valore totale di
aumentano il
valore totale di 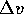 , per cui la soluzione piana è la migliore.
, per cui la soluzione piana è la migliore.
In alcuni casi, per h/R grande, esistono delle strategie con
incrementi di velocità distribuiti in tre impulsi (anziché due)
che risultano in un 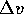 totale minore di quello dell'orbita di
Hohmann.
totale minore di quello dell'orbita di
Hohmann.
In pratica non è possibile lanciare con elevazione zero, sia perché il veicolo spaziale deve trovarsi al di sopra degli strati più densi dell'atmosfera prima di raggiungere velocità che darebbero luogo ad interazioni distruttive con il gas, sia per diminuire la perdita dovuta alla gravità durante la fase di accelerazione; perciò i lanci si effettuano verticalmente. Basta osservare attentamente la ripresa televisiva di un lancio per accorgersi che l'elevazione diminuisce rapidamente durante la fase di accelerazione, tanto che al momento del distacco del secondo stadio la traiettoria è quasi orizzontale.
Problema
Cerchiamo di calcolare la velocità e la direzione per un
lancio interplanetario . Se la velocità di lancio è 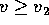 è possibile sfuggire al campo gravitazionale del pianeta di
partenza.
è possibile sfuggire al campo gravitazionale del pianeta di
partenza.
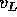 necessaria perché
il limite per
necessaria perché
il limite per 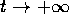 (e anche per
(e anche per 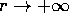 ) della
velocità sia un valore assegnato
) della
velocità sia un valore assegnato 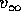 .
.
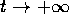 dell'angolo polare
dell'angolo polare 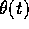 nel piano orbitale,
supponendo che il lancio avvenga con condizioni iniziali
nel piano orbitale,
supponendo che il lancio avvenga con condizioni iniziali
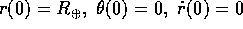 (elevazione nulla).
(elevazione nulla).
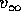 e la
direzione di fuga al variare dell'elevazione del lancio, nelle due
ipotesi che il pianeta non ruoti e che ruoti, con piattaforma di
lancio all'equatore.
e la
direzione di fuga al variare dell'elevazione del lancio, nelle due
ipotesi che il pianeta non ruoti e che ruoti, con piattaforma di
lancio all'equatore.
Suggerimento: Il limite per 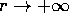 di E è semplicemente
di E è semplicemente 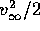 ,
da cui si deduce la formula
,
da cui si deduce la formula

La direzione dell'asintoto si deduce da
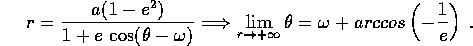
Esercizio
Calcolare gli elementi orbitali 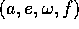 al lancio dalla
superficie R=1 di un pianeta con GM=1, con le seguenti velocità
ed elevazioni di lancio:
al lancio dalla
superficie R=1 di un pianeta con GM=1, con le seguenti velocità
ed elevazioni di lancio:
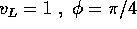
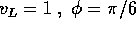
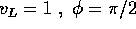
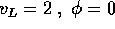
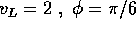 .
.
I pianeti orbitano tutti attorno al Sole (di massa 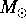 );
poiché la massa dei pianeti è molto più piccola di quella del
Sole, le soluzioni del problema dei due corpi Sole-pianeta sono buone
approssimazioni per le orbite dei pianeti. Le orbite risultano in
effetti ellittiche, ma con eccentricità da piccola a moderata
(soltanto per Mercurio e Plutone non è proprio possibile trascurare
l'eccentricità). Nei problemi che seguono sarà descritta una prima
approssimazione di una missione interplanetaria, per esempio dalla
Terra a Marte e ritorno.
);
poiché la massa dei pianeti è molto più piccola di quella del
Sole, le soluzioni del problema dei due corpi Sole-pianeta sono buone
approssimazioni per le orbite dei pianeti. Le orbite risultano in
effetti ellittiche, ma con eccentricità da piccola a moderata
(soltanto per Mercurio e Plutone non è proprio possibile trascurare
l'eccentricità). Nei problemi che seguono sarà descritta una prima
approssimazione di una missione interplanetaria, per esempio dalla
Terra a Marte e ritorno.
Per una presentazione suggestiva, anche se tecnologicamente datata, di una spedizione marziana si può consultare [Ley-von Braun 59]. Per una trattazione più ampia delle orbite interplanetarie, consultare [Roy 82].
Problema
Supponiamo che il pianeta di partenza abbia semiasse maggiore 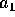 ed
eccentricità
ed
eccentricità 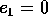 , mentre il pianeta di destinazione abbia
semiasse ed eccentricità
, mentre il pianeta di destinazione abbia
semiasse ed eccentricità 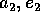 ; supponiamo per esempio
; supponiamo per esempio 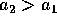 .
.
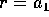 fino a
fino a 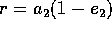 ; supponiamo cioè che
l'incontro con il pianeta di destinazione avvenga al perielio
(pericentro) di quest'ultimo.
; supponiamo cioè che
l'incontro con il pianeta di destinazione avvenga al perielio
(pericentro) di quest'ultimo.
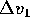 necessario per passare dall'orbita del primo pianeta a quella di
Hohmann, e quello
necessario per passare dall'orbita del primo pianeta a quella di
Hohmann, e quello 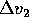 per immettersi nell'orbita del secondo
pianeta dall'orbita di Hohmann.
per immettersi nell'orbita del secondo
pianeta dall'orbita di Hohmann.
Problema
Il lancio dal pianeta di partenza viene descritto mediante
l'approssimazione a due corpi, con il pianeta supposto a simmetria
sferica di raggio 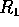 e di massa
e di massa 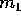 . L'orbita planetocentrica
(iperbolica) e quella eliocentrica di Hohmann vengono raccordate in
modo
. L'orbita planetocentrica
(iperbolica) e quella eliocentrica di Hohmann vengono raccordate in
modo 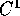 , come se si potesse passare istantaneamente da un
problema dei due corpi ad un altro. Come ulteriore semplificazione
si usa, per la velocità planetocentrica, quella asintotica
sull'iperbole, pur supponendo che la posizione sia
quella del pianeta. Nello stesso modo viene descritta la cattura
dall'orbita di Hohmann, interpretata come orbita iperbolica nel
sistema di riferimento che si muove con il secondo pianeta di
raggio
, come se si potesse passare istantaneamente da un
problema dei due corpi ad un altro. Come ulteriore semplificazione
si usa, per la velocità planetocentrica, quella asintotica
sull'iperbole, pur supponendo che la posizione sia
quella del pianeta. Nello stesso modo viene descritta la cattura
dall'orbita di Hohmann, interpretata come orbita iperbolica nel
sistema di riferimento che si muove con il secondo pianeta di
raggio 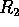 e massa
e massa 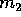 .
.
Questa approssimazione è sensata, perché per distanze abbastanza piccole dai pianeti la loro attrazione è maggiore di quella del Sole. Però non è affatto facile stimare rigorosamente l'errore commesso in questa approssimazione ``kepleriana a tratti'', che tuttavia conduce a risultati praticamente utilizzabili in quasi tutti i casi.
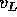 e, supponendo l'elevazione
e, supponendo l'elevazione
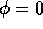 , trovare l'angolo rispetto al Sole del punto di lancio per
ottenere una velocità ``all'infinito'' con modulo
, trovare l'angolo rispetto al Sole del punto di lancio per
ottenere una velocità ``all'infinito'' con modulo 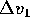 e
direzione lungo l'orbita del primo pianeta.
e
direzione lungo l'orbita del primo pianeta.
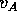 con cui la sonda interplanetaria
arriverà alla superficie del pianeta di destinazione, supponendo
che vi arrivi con elevazione nulla (cioè con pericentro ad
con cui la sonda interplanetaria
arriverà alla superficie del pianeta di destinazione, supponendo
che vi arrivi con elevazione nulla (cioè con pericentro ad 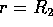 , dove r
è la distanza dal centro del secondo pianeta); trovare l'angolo
rispetto al Sole del punto di atterraggio.
, dove r
è la distanza dal centro del secondo pianeta); trovare l'angolo
rispetto al Sole del punto di atterraggio.
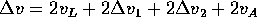 (se le velocità di arrivo devono essere
frenate attivamente) e come
(se le velocità di arrivo devono essere
frenate attivamente) e come 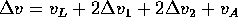 (se le velocità di arrivo sono frenate passivamente).
(se le velocità di arrivo sono frenate passivamente).
Problema
Semplifichiamo il problema assumendo 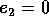 , in modo che il
risultato non dipenda dall'anomalia vera del secondo
pianeta. Vogliamo calcolare la durata totale di una missione
interplanetaria di andata e ritorno tra i due pianeti.
, in modo che il
risultato non dipenda dall'anomalia vera del secondo
pianeta. Vogliamo calcolare la durata totale di una missione
interplanetaria di andata e ritorno tra i due pianeti.
Suggerimento: La scala di tempi di questo tipo di missioni è dettata dal periodo sinodico

che è l'intervallo di tempo dopo il quale l'angolo pianeta 1-Sole-pianeta 2 si ripete.
Problema
Sia 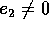 , e supponiamo ancora che l'incontro avvenga al perielio
del secondo pianeta.
, e supponiamo ancora che l'incontro avvenga al perielio
del secondo pianeta.
Il problema precedente è assai più difficile di quello relativo ad
orbite circolari, perché richiede di calcolare le effemeridi ,
cioè la legge oraria: se al tempo 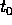 il secondo pianeta si trova
al perielio (cioè con
il secondo pianeta si trova
al perielio (cioè con 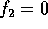 ), quale sarà la sua posizione al
tempo t? Questo calcolo può essere ridotto ad una quadratura , ma
la corrispondente primitiva non è esprimibile mediante funzioni
elementari. Perciò conviene far uso di una variabile intermedia:
l'anomalia eccentrica.
), quale sarà la sua posizione al
tempo t? Questo calcolo può essere ridotto ad una quadratura , ma
la corrispondente primitiva non è esprimibile mediante funzioni
elementari. Perciò conviene far uso di una variabile intermedia:
l'anomalia eccentrica.
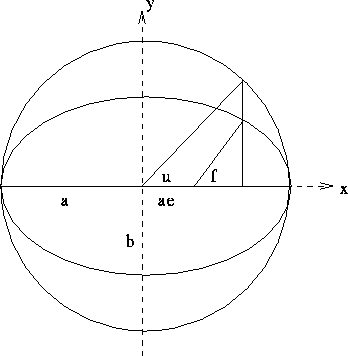
Figure 7.6: Definizione dell'anomalia eccentrica, in funzione
dell'anomalia vera e dell'eccentricità.
L'anomalia eccentrica si può interpretare geometricamente
dopo aver trasformato l'ellisse della traiettoria in una circonferenza
centrata nel punto medio dei due fuochi, per mezzo di una dilatazione di
un fattore 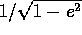 lungo l'asse minore;
l'anomalia eccentrica (vedi Figura 7.6) è
l'angolo visto dal centro della circonferenza fra la posizione ``dilatata'' ed il raggio
del pericentro. Analiticamente, la
relazione tra anomalia eccentrica u ed anomalia vera f
è definita attraverso l'espressione delle coordinate cartesiane, in un
riferimento (x,y) avente l'asse x orientato
lungo il vettore di Laplace-Lenz
e l'asse y nel piano orbitale, orientato in modo
che l'angolo polare nel piano (x,y) sia crescente con il tempo:
lungo l'asse minore;
l'anomalia eccentrica (vedi Figura 7.6) è
l'angolo visto dal centro della circonferenza fra la posizione ``dilatata'' ed il raggio
del pericentro. Analiticamente, la
relazione tra anomalia eccentrica u ed anomalia vera f
è definita attraverso l'espressione delle coordinate cartesiane, in un
riferimento (x,y) avente l'asse x orientato
lungo il vettore di Laplace-Lenz
e l'asse y nel piano orbitale, orientato in modo
che l'angolo polare nel piano (x,y) sia crescente con il tempo:
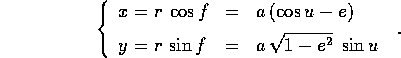
La legge della traiettoria si può quindi esprimere come relazione tra il raggio r e una delle due anomalie:
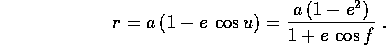
L'equazione che lega l'anomalia eccentrica al tempo si può ricavare usando la derivata rispetto al tempo del raggio, espressa nei due modi
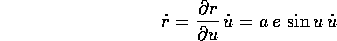
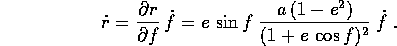
Sostituendo la legge delle aree 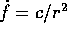 , il termine
, il termine 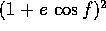 si semplifica:
si semplifica:
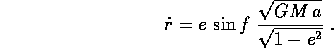
Confrontando le due espressioni, si ottiene
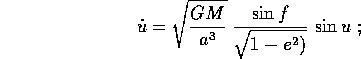
si può riconoscere nel primo fattore il moto medio n, e ricavando il secondo fattore dalle due espressioni per y si ha l'equazione a variabili separabili

da cui si ricava l'inversa della legge oraria
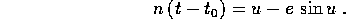
Poiché il tempo 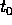 corrisponde ad u=0, e quindi anche ad f=0,
se definiamo una variabile angolo
corrisponde ad u=0, e quindi anche ad f=0,
se definiamo una variabile angolo

questa si identifica con l'anomalia media che appare nella parametrizzazione del problema dei due corpi in variabili azione-angolo . Perciò la relazione tra l'anomalia eccentrica e l'anomalia media è l'equazione di Keplero

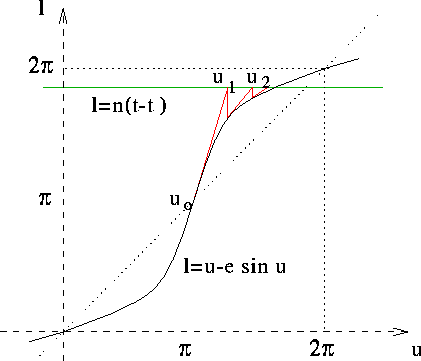
Figure 7.7: L'equazione di Keplero: risolvere rispetto
all'anomalia eccentrica vuol dire trovare l'intersezione di una retta
orizzontale (con anomalia media costante) con la curva che rappresenta
il secondo membro. Il metodo di Newton usa le intersezioni della retta
orizzontale con le tangenti alla curva come approssimazioni
successive. Il punto corrispondente all'apocentro è l'unico punto di
flesso (tra i valori principali); se usato come condizione iniziale
evita qualsiasi cambio da convessità a concavità, quindi rende la
convergenza certa.
L'equazione di Keplero fornisce immediatamente l'inversa della legge
oraria: data l'anomalia vera, si calcola quella eccentrica con le
formule per (x,y), e da questa l'anomalia media che fornisce il
tempo al quale corrisponde la direzione data. Se però si vuole
trovare la direzione f ad un tempo t dato, occorre calcolare la
funzione inversa, cioè risolvere l'equazione di Keplero rispetto ad
u. Questo non si può fare analiticamente (con funzioni
elementari), ma esiste un procedimento numerico inventato da Newton
appositamente per risolvere l'equazione di Keplero. Il
metodo di Newton consiste nel costruire una successione di
approssimazioni successive 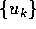 a partire da una prima
approssimazione
a partire da una prima
approssimazione 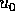 , utilizzando la linearizzazione dell'equazione
in ogni punto:
, utilizzando la linearizzazione dell'equazione
in ogni punto:
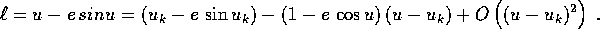
Se si trascurano i termini del secondo ordine,
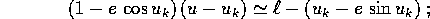
allora si definisce la successione 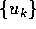 per ricorrenza mediante
per ricorrenza mediante
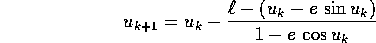
e si ottiene una successione che, pur di scegliere opportunamente
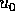 , converge molto rapidamente verso un limite che è la
soluzione. La scelta di
, converge molto rapidamente verso un limite che è la
soluzione. La scelta di 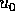 si può fare con vari metodi, ma la
scelta più sicura è quella di porre
si può fare con vari metodi, ma la
scelta più sicura è quella di porre 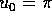 ; per ragioni di
convessità, evidenti dalla Figura 7.7, con questa
scelta il metodo di Newton converge per ogni e<1 e per ogni
; per ragioni di
convessità, evidenti dalla Figura 7.7, con questa
scelta il metodo di Newton converge per ogni e<1 e per ogni 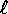 con
con 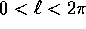 .
.
Problema
Supponiamo di voler estendere l'esplorazione del sistema solare ai
pianeti più lontani. A questo scopo si vuole iniettare il veicolo
spaziale in un'orbita parabolica (o iperbolica) che consente di
arrivare ad una qualunque distanza data. Sempre partendo da un'orbita
con semiasse maggiore 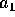 ed eccentricità
ed eccentricità 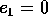 , calcolare
(in funzione della massa solare
, calcolare
(in funzione della massa solare 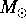 ) il minimo incremento di
velocità
) il minimo incremento di
velocità 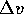 necessario per sfuggire al campo
gravitazionale del Sole.
necessario per sfuggire al campo
gravitazionale del Sole.
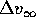 , con la stessa direzione della velocità
(generalizzazione dell'orbita di trasferimento di Hohmann
per
, con la stessa direzione della velocità
(generalizzazione dell'orbita di trasferimento di Hohmann
per 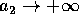 ).
).
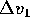 per immettersi nell'orbita di Hohmann
che consente di incrociare un altro pianeta con semiasse
per immettersi nell'orbita di Hohmann
che consente di incrociare un altro pianeta con semiasse 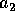 ,
eccentricità
,
eccentricità 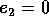 , massa
, massa 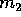 e raggio
e raggio 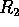 ; quindi
utilizzare l'assistenza gravitazionale del pianeta per
ottenere (nell'approssimazione kepleriana a tratti) un incremento di
velocità
; quindi
utilizzare l'assistenza gravitazionale del pianeta per
ottenere (nell'approssimazione kepleriana a tratti) un incremento di
velocità 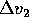 sufficiente ad entrare in un'orbita
illimitata. In questo modo il consumo di propellente corrisponde
solo a
sufficiente ad entrare in un'orbita
illimitata. In questo modo il consumo di propellente corrisponde
solo a 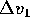 , e d è quindi minore di quello del caso (I).
, e d è quindi minore di quello del caso (I).
Suggerimento: Il massimo incremento di velocità ricevuto passando vicino
ad un pianeta si ottiene supponendo che il pericentro dell'orbita
iperbolica planetocentrica abbia raggio 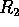 , e
calcolando il cambiamento di velocità fra l'asintoto in entrata e
quello in uscita. Per calcolare il cambiamento
, e
calcolando il cambiamento di velocità fra l'asintoto in entrata e
quello in uscita. Per calcolare il cambiamento 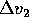 nel modulo
della velocità, assumere che gli asintoti dell'orbita iperbolica
planetocentrica abbiano per bisettrice la tangente all'orbita di
nel modulo
della velocità, assumere che gli asintoti dell'orbita iperbolica
planetocentrica abbiano per bisettrice la tangente all'orbita di
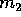 .
.
Per essere in grado di riconoscere grandezze dotate di senso fisico e ingegneristico nelle formule dell'astrodinamica, come quelle ricavate dai problemi di questa Sezione, occorre definire le unità di misura impiegate. Ci sono fondamentalmente due scelte possibili: si può usare il sistema metrico decimale, magari con unità chilometri e secondi; oppure si possono usare unità di tempo legate alle grandezze in gioco, come l'unità astronomica e l'anno, oppure il raggio della Terra e il giorno.
In astrodinamica si misurano essenzialmente soltanto lunghezze e tempi, nella descrizione delle orbite e delle manovre; la misure di masse intervengono solo nella descrizione del veicolo spaziale e delle sue parti, e per questo scopo si impiegano unità di uso comune come il chilogrammo-massa. Infatti nelle equazioni di moto di un corpo di massa trascurabile (rispetto ai corpi attrattori) non appare mai una massa M se non accompagnata dal fattore G, la costante di gravitazione universale . Il prodotto GM ha la dimensione di una lunghezza al cubo divisa per un tempo al quadrato: in simboli,

perciò il valore di GM non dipende dalla scelta dell'unità di massa. Per esempio per la Terra un valore, misurato recentemente dalle orbite dei satelliti artificiali, è
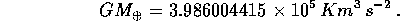
Per dedurre da questo valore di 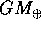 la massa della Terra
la massa della Terra
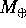 espressa in unità metriche decimali, occorre conoscere il
valore ``di laboratorio'' della
costante di gravitazione universale in unità metriche.
Poiché l'interazione
gravitazionale è molto debole tra corpi che un comune laboratorio
possa contenere, la misura di G è molto difficile: la migliore
stima basata su esperimenti anche recenti è
espressa in unità metriche decimali, occorre conoscere il
valore ``di laboratorio'' della
costante di gravitazione universale in unità metriche.
Poiché l'interazione
gravitazionale è molto debole tra corpi che un comune laboratorio
possa contenere, la misura di G è molto difficile: la migliore
stima basata su esperimenti anche recenti è
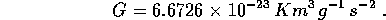
Perciò una scelta valida per lo studio di satelliti artificiali è
l'uso di chilometri e secondi come unità, usando un valore di
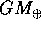 come quello citato sopra. Una recente misura del raggio
equatoriale della Terra è
come quello citato sopra. Una recente misura del raggio
equatoriale della Terra è
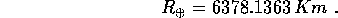
Esercizio Calcolare la prima velocità cosmica e la velocità di fuga per la Terra in Km/s.
La scelta opposta può essere conveniente per lo studio delle
traiettorie interplanetarie. Per le lunghezze si definisce
l'unità astronomica (simbolo AU)
come il semiasse maggiore dell'orbita di un
pianeta che abbia periodo di un anno (più precisamente, un anno
convenzionale di 365.25 giorni di 86400 secondi), nell'ipotesi che la
costante 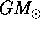 abbia il valore convenzionale
abbia il valore convenzionale
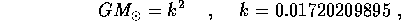
dove la costante k è detta costante di Gauss . Come l'unità di misura dei tempi, si sceglie il giorno d ``delle effemeridi'', esattamente pari ad 86400 secondi.
La costante k fu determinata appunto da Gauss con i migliori dati disponibili alla sua epoca, in modo che l'unità astronomica corrispondesse al semiasse maggiore della Terra; una volta fissata questa convenzione sull'unità di misura, il semiasse maggiore della Terra è una quantità da misurare, e la migliore stima attuale è
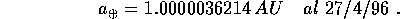
È chiaro però che, se si usano due diversi sistemi di unità di
misura, bisogna disporre di un procedimento per trasformare tutti i
risultati dei nostri calcoli da un sistema all'altro. Per esempio, il
lancio di una missione interplanetaria può essere calcolato in
unità (Km, s) e l'orbita di trasferimento interplanetaria
calcolata in (AU, d), e allora la velocità di uscita dal
campo gravitazionale della Terra 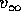 deve essere riscalata.
deve essere riscalata.
Un cambiamento di scala è una trasformazione in cui tutte le
variabili, e le loro funzioni, sono moltiplicati per fattori di
scala (numeri reali positivi) dipendenti dalle loro
dimensioni. Per esempio, se le lunghezze sono moltiplicate per 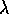 ,
i tempi per
,
i tempi per  , le masse per
, le masse per 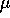 , allora le velocità vanno
moltiplicate per
, allora le velocità vanno
moltiplicate per 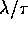 , e la costante di gravitazione
universale G va moltiplicata per
, e la costante di gravitazione
universale G va moltiplicata per

che altro non è che la terza legge di Keplero (i cubi delle dimensioni lineari delle orbite sono proporzionali ai quadrati dei periodi).
Anche se una mappa di uno spazio in se stesso può essere interpretata sia come trasformazione dei punti dello spazio, sia come un cambiamento di coordinate che descrive gli stessi punti in coordinate diverse, un cambiamento di scala viene comunemente interpretato come la descrizione delle stesse grandezze con unità di misura diverse, non come un cambiamento effettivo.
Per passare dal sistema (AU, d) al sistema (Km,s) basta dunque
sapere che un giorno delle effemeridi è esattamente 86400 secondi
(quindi 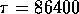 ) e che
) e che 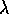 è il valore in chilometri di una
AU: una stima recente è
è il valore in chilometri di una
AU: una stima recente è
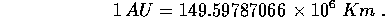
Esercizio
Calcolare 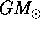 , che vale
, che vale 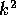 in unità (AU,d), nelle
unità (Km,s); dal valore di G in quest'ultimo sistema, dedurre
la massa del Sole in grammi.
in unità (AU,d), nelle
unità (Km,s); dal valore di G in quest'ultimo sistema, dedurre
la massa del Sole in grammi.
In calcoli semplificati, del tipo usato per una prima approssimazione
nel progetto di missioni spaziali, si possono anche usare come unità l'AU
e l'anno y, ed approssimare la costante 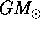 con
con 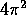 :
allora la terza legge di Keplero
:
allora la terza legge di Keplero
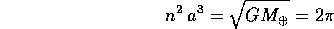
fornisce un periodo 1 anno per un'orbita di raggio 1 AU.
Questa ultima formula contiene l'approssimazione per cui si trascura la massa del pianeta, anziché usare il problema dei due corpi Sole-pianeta. L'errore è dell'ordine di una parte su 1000 o meno, secondo il pianeta.
Esercizio
Calcolare la velocità orbitale della Terra 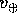 , supponendo
, supponendo
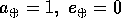 , in Km/s. Calcolare la velocità di
fuga dal sistema solare
, in Km/s. Calcolare la velocità di
fuga dal sistema solare 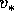 partendo dall'orbita terrestre.
partendo dall'orbita terrestre.
Suggerimento: Limitarsi all'approssimazione 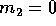 ed usare le unità
(AU,y), quindi riscalare.
ed usare le unità
(AU,y), quindi riscalare.
Esercizio Calcolare la terza velocità cosmica sufficiente per far uscire dal sistema solare una sonda lanciata dalla superficie della Terra, usando l'approssimazione kepleriana a tratti, in km/s.
Suggerimento: Imporre che la velocità
asintotica 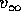 all'uscita dal campo gravitazionale terrestre
sia pari a
all'uscita dal campo gravitazionale terrestre
sia pari a  .
.
Problema
Ricalcolare la
terza velocità cosmica
nel caso che il lancio sfrutti l'assistenza gravitazionale di Giove,
verificando che quest'ultima sia sufficiente a trasferire
dall'orbita di Hohmann per Giove ad un'orbita iperbolica. Si usino i
dati approssimati 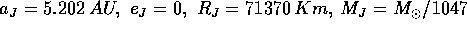 .
.
Gli incrementi di velocità che un lancio spaziale o una manovra richiedono per il cambiamento di un'orbita, risultano dall'uso di un sistema di propulsione. Si conoscono soltanto due tipi di sistemi di propulsione che funzionano nello spazio (esterno all'atmosfera): il razzo e la vela solare . Poiché il secondo non è ancora praticamente in uso, ci limitiamo a discutere i razzi, mostrando soltanto come ricondurre il calcolo dell'efficacia di un razzo alle leggi della meccanica fin qui studiata
Supponiamo che un veicolo spaziale in moto libero (non soggetto ad
alcuna forza esterna) abbia una massa dipendente dal tempo m(t), con
valore iniziale 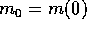 , e supponiamo che la massa perduta sia
interamente impiegata come massa di scarico di un razzo, che viene
espulsa ad una velocità V relativamente al veicolo, in direzione
opposta a quella della traiettoria della massa restante.
Supponendo che il moto sia
unidimensionale e che il razzo sia puntato sempre nella stessa
direzione, dalla
conservazione della quantità di moto si deduce
l'equazione del razzo : se x(t) è la coordinata del
veicolo spaziale
e v(t)=dx/dt(t) la velocità,
, e supponiamo che la massa perduta sia
interamente impiegata come massa di scarico di un razzo, che viene
espulsa ad una velocità V relativamente al veicolo, in direzione
opposta a quella della traiettoria della massa restante.
Supponendo che il moto sia
unidimensionale e che il razzo sia puntato sempre nella stessa
direzione, dalla
conservazione della quantità di moto si deduce
l'equazione del razzo : se x(t) è la coordinata del
veicolo spaziale
e v(t)=dx/dt(t) la velocità,
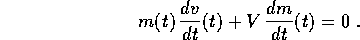
Se supponiamo di conoscere il funzionamento del razzo, cioè la
velocità di scarico V e la funzione m(t), allora
la velocità può essere calcolata con una semplice quadratura
a partire dalla condizione iniziale 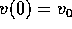 :
:
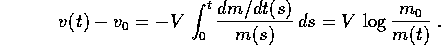
Perciò se il rapporto di massa è 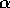 , cioè la massa
disponibile come propellente è
, cioè la massa
disponibile come propellente è  con
con 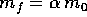 , al
termine della fase propulsiva la massa finale
, al
termine della fase propulsiva la massa finale 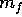 viaggerà con la
velocità
viaggerà con la
velocità

Senza entrare in complicati problemi tecnici, è chiaro che il
rapporto di massa 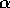 è limitato dalla presenza, nella massa
finale, del sistema propulsivo stesso. Perciò valori di
è limitato dalla presenza, nella massa
finale, del sistema propulsivo stesso. Perciò valori di 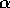 molto grandi si ottengono in pratica soltanto in un sistema a più
stadi, in cui la massa finale
molto grandi si ottengono in pratica soltanto in un sistema a più
stadi, in cui la massa finale 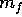 comprende un
secondo stadio con un sistema propulsivo più piccolo, che
può a sua volta incrementare la velocità di
comprende un
secondo stadio con un sistema propulsivo più piccolo, che
può a sua volta incrementare la velocità di 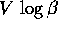 riducendo la massa del veicolo a
riducendo la massa del veicolo a 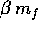 , e così via.
, e così via.
Per avere un'idea delle grandezze in gioco, si tenga presente
che il valore della velocità di scarico V dipende dalla tecnologia
impiegata: per motori recenti oscilla tipicamente da circa 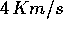 per razzi chimici fino a
per razzi chimici fino a 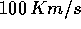 per propulsori elettrici
a ioni. Così un razzo chimico ad un solo stadio con rapporto di
massa
per propulsori elettrici
a ioni. Così un razzo chimico ad un solo stadio con rapporto di
massa 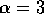 può raggiungere circa
può raggiungere circa 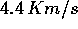 , con un secondo
stadio può raggiungere la seconda velocità cosmica, con tre stadi
può raggiungere la terza velocità cosmica, con un rapporto di
massa finale
, con un secondo
stadio può raggiungere la seconda velocità cosmica, con tre stadi
può raggiungere la terza velocità cosmica, con un rapporto di
massa finale 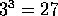 . Questo valore teorico è naturalmente
ottimistico, perché non abbiamo tenuto conto delle perdite dovute
alla gravità (cioè al fatto che mentre il razzo sta accelerando
verso l'alto sta anche perdendo velocità per effetto
dell'accelerazione di gravità g), né abbiamo tenuto conto
dell'atmosfera che influisce anche sulla velocità di scarico,
eccetera. Tuttavia, i semplici calcoli basati sulla sola equazione del
razzo e sulle approssimazioni kepleriane - o kepleriane a tratti-
sono sufficienti a dare un'idea degli ordini di grandezza che
compaiono nella progettazione di missioni spaziali.
. Questo valore teorico è naturalmente
ottimistico, perché non abbiamo tenuto conto delle perdite dovute
alla gravità (cioè al fatto che mentre il razzo sta accelerando
verso l'alto sta anche perdendo velocità per effetto
dell'accelerazione di gravità g), né abbiamo tenuto conto
dell'atmosfera che influisce anche sulla velocità di scarico,
eccetera. Tuttavia, i semplici calcoli basati sulla sola equazione del
razzo e sulle approssimazioni kepleriane - o kepleriane a tratti-
sono sufficienti a dare un'idea degli ordini di grandezza che
compaiono nella progettazione di missioni spaziali.
Per illustrare l'applicazione delle leggi della meccanica a problemi di una certa importanza pratica, nei problemi che seguono si studierà il comportamento dei missili balistici , che compiono una traiettoria controllata sostanzialmente solo dalla gravità dopo il lancio. Si suppone di usare l'approssimazione del problema dei due corpi, con la Terra a simmetria sferica, e si considera il lancio istantaneo.
Problema
Calcolare la velocità di lancio 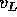 (in Km/s) e
l'elevazione
(in Km/s) e
l'elevazione 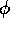 necessarie per il
lancio di un missile intercontinentale
che parta da
necessarie per il
lancio di un missile intercontinentale
che parta da 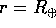 e ritorni a cadere
sulla superficie
e ritorni a cadere
sulla superficie 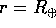 ad una distanza angolare (l'angolo
fra le due posizioni visto dal centro della Terra) pari a
ad una distanza angolare (l'angolo
fra le due posizioni visto dal centro della Terra) pari a
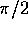 .
.
Suggerimento: L'orbita ellittica
deve essere percorsa per valori dell'anomalia vera tra 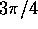 e
e
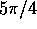 . Dall'equazione del raggio in funzione dell'anomalia vera
dedurre una relazione tra a ed e, quindi minimizzare
. Dall'equazione del raggio in funzione dell'anomalia vera
dedurre una relazione tra a ed e, quindi minimizzare 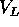 attraverso la relazione con a dedotta dalla formula dell'energia.
attraverso la relazione con a dedotta dalla formula dell'energia.
Si noti che il valore della velocità di lancio richiesta non è molto inferiore alla prima velocità cosmica .
Problema
Calcolare il tempo necessario 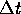 per il percorso descritto
nel problema precedente.
per il percorso descritto
nel problema precedente.
Suggerimento: L'orbita ellittica calcolata nel
problema precedente deve essere percorsa da 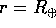 al ritorno
ad
al ritorno
ad 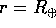 . Calcolare i valori corrispondenti dell'anomalia
media, ed usare l'equazione di Keplero per trovare
l'anomalia media e quindi il tempo.
. Calcolare i valori corrispondenti dell'anomalia
media, ed usare l'equazione di Keplero per trovare
l'anomalia media e quindi il tempo.
Il tempo di volo calcolato nel problema precedente dà un'idea
della scala di tempi di una guerra nucleare globale, la cui durata
difficilmente potrebbe eccedere 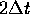 .
.
Problema
Supponiamo che siano disponibili razzi con velocità di
scarico 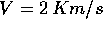 .
.
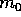 di un missile
balistico intercontinentale capace di lanciare ad una
distanza angolare
di un missile
balistico intercontinentale capace di lanciare ad una
distanza angolare
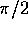 sulla superficie della terra un carico di
sulla superficie della terra un carico di 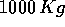 .
.
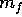 del missile di cui
al punto (I) sia utilizzata per un ulteriore stadio, calcolare il
valore del rapporto di massa
del missile di cui
al punto (I) sia utilizzata per un ulteriore stadio, calcolare il
valore del rapporto di massa 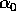 necessario per raggiungere
la prima velocità cosmica, ed il valore
necessario per raggiungere
la prima velocità cosmica, ed il valore 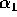 richiesto per
lanciare un satellite su un'orbita circolare ad un'altezza
richiesto per
lanciare un satellite su un'orbita circolare ad un'altezza
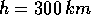 .
.
Il problema precedente consiste, in altre parole, nel calcolare quali satelliti si possono lanciare aggiungendo un terzo stadio ad un missile balistico intercontinentale; questo problema era di grande attualità nell'ottobre del 1957, al momento del lancio di Sputnik I, il primo satellite artificiale.
Per una trattazione approfondita delle traiettorie dei missili balistici, si può consultare il libro di testo usato dalla United States Air Force Academy [Bate et al. 71].
Problema
Ad una distanza di 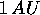 dal Sole, il flusso di radiazione
elettromagnetica dal Sole ha un'intensità
dal Sole, il flusso di radiazione
elettromagnetica dal Sole ha un'intensità 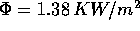 (la cosiddetta costante solare ). La quantità di
moto p trasportata dalla luce p è legata all'energia E
contenuta nella luce stessa da E=pc (dove
(la cosiddetta costante solare ). La quantità di
moto p trasportata dalla luce p è legata all'energia E
contenuta nella luce stessa da E=pc (dove 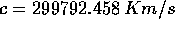 è la
velocità della luce): ne segue che una superficie perfettamente
riflettente ortogonale al flusso (situazione in cui il momento
scambiato con la radiazione
raddoppia), la cui area sia A, riceve una spinta pari a
è la
velocità della luce): ne segue che una superficie perfettamente
riflettente ortogonale al flusso (situazione in cui il momento
scambiato con la radiazione
raddoppia), la cui area sia A, riceve una spinta pari a

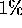 dell'accelerazione dovuta all'attrazione del Sole. Calcolare lo spessore che
dovrebbe avere la vela, supponendo la densità 1.
dell'accelerazione dovuta all'attrazione del Sole. Calcolare lo spessore che
dovrebbe avere la vela, supponendo la densità 1.
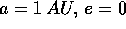 ? Sarebbe possibile impiegare un
simile veicolo per la navigazione interplanetaria, controllando
l'angolo formato dalla
vela con il flusso di radiazione solare ?
? Sarebbe possibile impiegare un
simile veicolo per la navigazione interplanetaria, controllando
l'angolo formato dalla
vela con il flusso di radiazione solare ?