



Next: 8.6 EQUAZIONI ALLE VARIAZIONI
Up: 8 EQUAZIONI DIFFERENZIALI DIPENDENTI
Previous: 8.4 SISTEMI A COEFFICIENTI
Sommario Se la dipendenza dal tempo è periodica, il comportamento
delle soluzioni può essere studiato tramite la mappa che descrive la
trasformazione delle condizioni iniziali nelle soluzioni dopo un
periodo. In questo modo si possono individuare le soluzioni periodiche
(con lo stesso periodo), e discutere la loro stabilità. Nel caso
lineare questa procedura fornisce un metodo di calcolo esplicito per
decidere la stabilità delle soluzioni periodiche.
Le soluzioni di sistemi di equazioni differenziali (non
necessariamente lineari) con secondi membri periodici (rispetto al
tempo) hanno delle proprietà valide in generale, che ci serviranno
poi nel caso lineare.
Proprietà:
Lo studio della stabilità delle soluzioni del sistema a coefficienti
periodici può
essere ricondotto a quello della stabilità di B, nel senso di
seguito precisato.
Definizione:
Teorema delle soluzioni periodiche :
Sia F(X,t) periodica nel tempo con periodo T. Se il flusso del
sistema 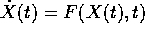 è definito per ogni
è definito per ogni 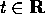 , e
, e
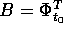 , allora
, allora
- la soluzione X(t) passante per
 è periodica di periodo
T se e solo se
è periodica di periodo
T se e solo se  è un punto fisso di B (
è un punto fisso di B ( 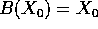 ), ed
è stabile (asintoticamente) se e solo se B è una
applicazione stabile (asintoticamente ) in
), ed
è stabile (asintoticamente) se e solo se B è una
applicazione stabile (asintoticamente ) in  ;
; - se F(X,t)=A(t)X è anche lineare in X, allora B è
lineare e
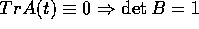 .
.
Dimostrazione:
-
-
Sia X(t) la soluzione periodica che parte da
 al tempo
al tempo 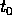 :
allora
:
allora 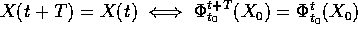 . Ma
. Ma
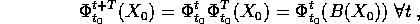
ovvero, ricordando che 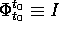 ,
,
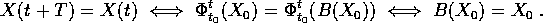
Inoltre, se la soluzione periodica X(t) passante per  è
stabile, le traiettorie che partono vicino a
è
stabile, le traiettorie che partono vicino a  tornano
periodicamente in un suo intorno: ovvero B è stabile in quanto, per ogni n:
tornano
periodicamente in un suo intorno: ovvero B è stabile in quanto, per ogni n:
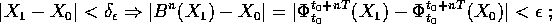
se X(t) è asintoticamente stabile, lo è anche B perché si
può passare al limite per 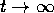 .
.
Viceversa, se è stabile B e X(t) è periodica, le traiettorie
che partono vicino a  non si discostano molto da X(t):
posto
non si discostano molto da X(t):
posto
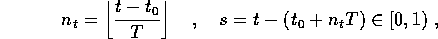
si ha, per la
continuità della dipendenza del flusso dalle condizioni iniziali,
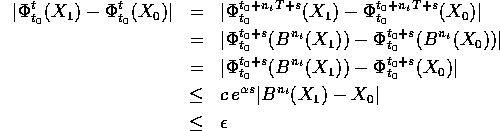
se 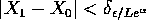 ; se B è asintoticamente
stabile, il maggiorante
; se B è asintoticamente
stabile, il maggiorante 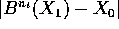 tende a 0 per
tende a 0 per 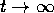 .
.
Nel caso lineare, la linearità di 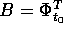 discende da quella
del flusso integrale; usando il teorema del determinante
wronskiano per calcolare
discende da quella
del flusso integrale; usando il teorema del determinante
wronskiano per calcolare 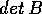 , da Tr A(t)=0 segue
, da Tr A(t)=0 segue
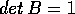 .
.
C.D.D.
I risultati precedenti si applicano in particolare allo studio di
alcune equazioni a coefficienti periodici che siano lineari.
Il moto (piccole oscillazioni) di un pendolo piano con
lunghezza variabile in
modo periodico è
governato (in assenza di dissipazione) dall'equazione
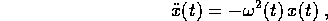
con 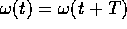 (si suppone
(si suppone 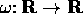 ) per un
T>0, ovvero dal sistema
) per un
T>0, ovvero dal sistema

in cui l'origine corrisponde alla posizione di equilibrio 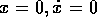 . Poiché Tr A(t)=0, per il teorema delle
soluzioni periodiche , l'applicazione B è lineare e
conserva l'area .
. Poiché Tr A(t)=0, per il teorema delle
soluzioni periodiche , l'applicazione B è lineare e
conserva l'area .
Le soluzioni del sistema sono stabili intorno all'origine se e solo se
B è stabile, ovvero se e solo se le parti reali dei suoi
autovalori hanno valore assoluto non superiore a 1, ossia se e solo
se vale il criterio della traccia |Tr B|<2; in tal
caso, infatti, poiché 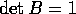 gli autovalori B sono complessi
coniugati, e la loro comune parte reale è pari a (Tr B/2) che
è in modulo minore di 1 (se invece sono reali e distinti non
possono avere entrambi modulo minore di 1).
gli autovalori B sono complessi
coniugati, e la loro comune parte reale è pari a (Tr B/2) che
è in modulo minore di 1 (se invece sono reali e distinti non
possono avere entrambi modulo minore di 1).
In particolare Tr, come funzione che associa valori reali alle
funzioni continue  per mezzo della matrice B,
è un operatore continuo (è continua la somma)
per mezzo della matrice B,
è un operatore continuo (è continua la somma) 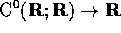 :
allora
l'insieme
:
allora
l'insieme 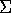 delle funzioni continue
delle funzioni continue  per le
quali il sistema è stabile
per le
quali il sistema è stabile
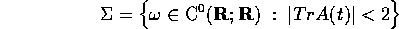
è un aperto dello spazio 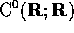 (immagine inversa dell'aperto
(-2,2)). In altre parole, perturbando un
(immagine inversa dell'aperto
(-2,2)). In altre parole, perturbando un  corrispondente ad un sistema stabile si ottiene un nuovo sistema
ancora stabile: si parla in tal caso di sistema
fortemente stabile .
corrispondente ad un sistema stabile si ottiene un nuovo sistema
ancora stabile: si parla in tal caso di sistema
fortemente stabile .
Esempio:
-
- Quanto sopra permette di studiare la stabilità intorno all'origine
di una classe di equazioni a coefficienti quasi costanti del
tipo
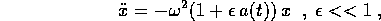
in funzione dei parametri  ed
ed  . Si suppone a(t)
periodica con periodo
. Si suppone a(t)
periodica con periodo 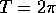 ed
ed  nel senso che
nel senso che
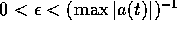 : è il caso, per esempio, di
un'altalena, ossia delle piccole oscillazioni di un pendolo con
frequenza variabile di poco intorno ad un valore medio
: è il caso, per esempio, di
un'altalena, ossia delle piccole oscillazioni di un pendolo con
frequenza variabile di poco intorno ad un valore medio  .
.
La figura 8.6 indica, nel piano di coordinate 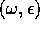 , le zone corrispondenti alle coppie di parametri che
individuano un sistema stabile intorno all'origine: la zona
tratteggiata è l'insieme per cui |Tr B|<2.
, le zone corrispondenti alle coppie di parametri che
individuano un sistema stabile intorno all'origine: la zona
tratteggiata è l'insieme per cui |Tr B|<2.
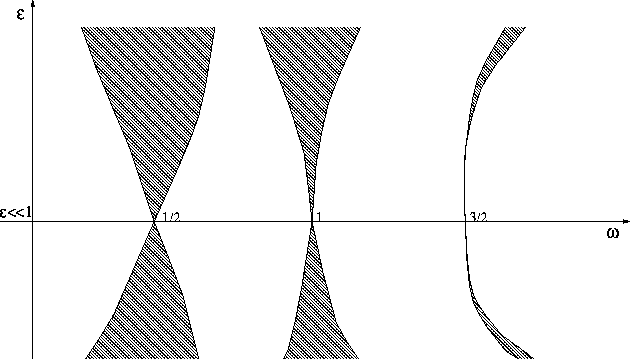
Figure 8.6: Risonanza parametrica: nel caso 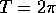 e
e
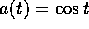 , sono tratteggiate le zone di stabilità,
corrispondenti a |Tr B|<2.
, sono tratteggiate le zone di stabilità,
corrispondenti a |Tr B|<2.
È evidente che per certi valori dei parametri in prossimità di
multipli seminteri della frequenza propria dell'altalena
( 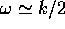 , con
, con 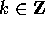 ) la posizione di equilibrio
inferiore è instabile: cioè una variazione periodica dei valori
dei parametri permette di dondolarsi sull'altalena. Il fenomeno è
detto della risonanza parametrica .
) la posizione di equilibrio
inferiore è instabile: cioè una variazione periodica dei valori
dei parametri permette di dondolarsi sull'altalena. Il fenomeno è
detto della risonanza parametrica .
A tale conclusione si giunge studiando la condizione |Tr B|<2
nell'intorno dei punti sull'asse  (
( 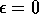 ), in
corrispondenza dei quali il problema è lineare e B può essere
esplicitamente calcolato:
), in
corrispondenza dei quali il problema è lineare e B può essere
esplicitamente calcolato:
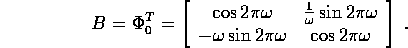
Allora 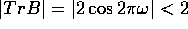 se
se 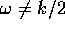 ; perciò il
dominio d'instabilità interseca l'asse
; perciò il
dominio d'instabilità interseca l'asse  solamente nei punti
solamente nei punti
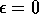 ,
, 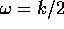 .
.




Next: 8.6 EQUAZIONI ALLE VARIAZIONI
Up: 8 EQUAZIONI DIFFERENZIALI DIPENDENTI
Previous: 8.4 SISTEMI A COEFFICIENTI
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
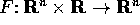 periodica nella seconda variabile,
ossia esista un periodo T>0 tale che F(X,t)=F(X,t+T) per
ogni
periodica nella seconda variabile,
ossia esista un periodo T>0 tale che F(X,t)=F(X,t+T) per
ogni 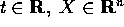 . Se il flusso del sistema
. Se il flusso del sistema 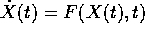 è definito per ogni
è definito per ogni 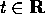 , allora
, allora
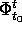 è invariante rispetto alle traslazioni di T
sull'asse dei tempi:
è invariante rispetto alle traslazioni di T
sull'asse dei tempi:

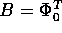 l'insieme di trasformazioni
l'insieme di trasformazioni
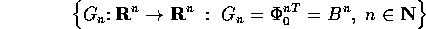
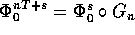 .
.
 ai tempi
ai tempi
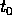 e
e 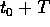 (nei rispettivi spazi delle fasi).
Sia
(nei rispettivi spazi delle fasi).
Sia 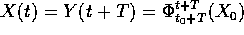 , dove
, dove
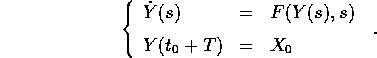
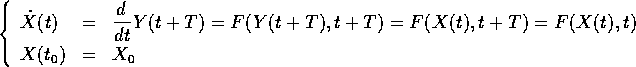
 al tempo
al tempo
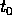 ,
, 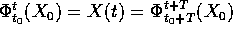 per ogni
per ogni
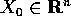 , ovvero
, ovvero 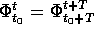 .
.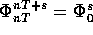 , si ha
, si ha
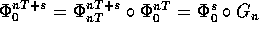 .
.
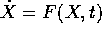 ,
, 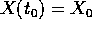 ,
si dice che
,
si dice che 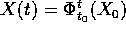 è
è
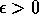 esiste un
esiste un 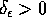 tale che:
tale che:
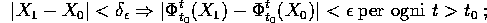
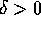 tale che:
tale che:
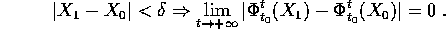
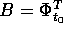 , allora
, allora
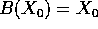 ), ed
è stabile (asintoticamente) se e solo se B è una
), ed
è stabile (asintoticamente) se e solo se B è una
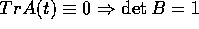 .
.
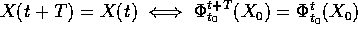 . Ma
. Ma
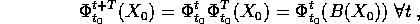
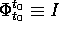 ,
,
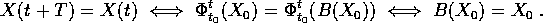
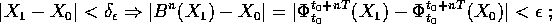
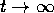 .
.
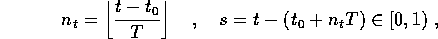
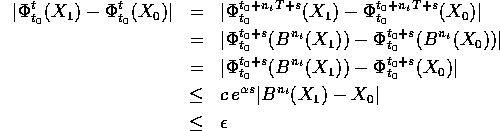
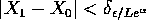 ; se B è asintoticamente
stabile, il maggiorante
; se B è asintoticamente
stabile, il maggiorante 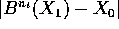 tende a 0 per
tende a 0 per 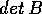 , da Tr A(t)=0 segue
, da Tr A(t)=0 segue
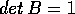 .
.
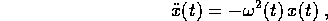
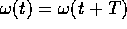 (si suppone
(si suppone 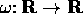 ) per un
T>0, ovvero dal sistema
) per un
T>0, ovvero dal sistema

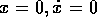 . Poiché Tr A(t)=0, per il teorema delle
. Poiché Tr A(t)=0, per il teorema delle
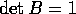 gli autovalori B sono complessi
coniugati, e la loro comune parte reale è pari a (Tr B/2) che
è in modulo minore di 1 (se invece sono reali e distinti non
possono avere entrambi modulo minore di 1).
gli autovalori B sono complessi
coniugati, e la loro comune parte reale è pari a (Tr B/2) che
è in modulo minore di 1 (se invece sono reali e distinti non
possono avere entrambi modulo minore di 1).
 per mezzo della matrice B,
è un operatore continuo (è continua la somma)
per mezzo della matrice B,
è un operatore continuo (è continua la somma) 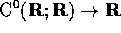 :
allora
l'insieme
:
allora
l'insieme 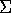 delle funzioni continue
delle funzioni continue 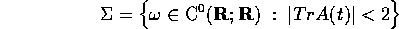
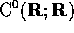 (immagine inversa dell'aperto
(-2,2)). In altre parole, perturbando un
(immagine inversa dell'aperto
(-2,2)). In altre parole, perturbando un 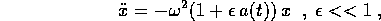
 . Si suppone a(t)
periodica con periodo
. Si suppone a(t)
periodica con periodo  ed
ed  nel senso che
nel senso che
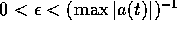 : è il caso, per esempio, di
un'altalena, ossia delle piccole oscillazioni di un pendolo con
frequenza variabile di poco intorno ad un valore medio
: è il caso, per esempio, di
un'altalena, ossia delle piccole oscillazioni di un pendolo con
frequenza variabile di poco intorno ad un valore medio 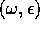 , le zone corrispondenti alle coppie di parametri che
individuano un sistema stabile intorno all'origine: la zona
tratteggiata è l'insieme per cui |Tr B|<2.
, le zone corrispondenti alle coppie di parametri che
individuano un sistema stabile intorno all'origine: la zona
tratteggiata è l'insieme per cui |Tr B|<2.
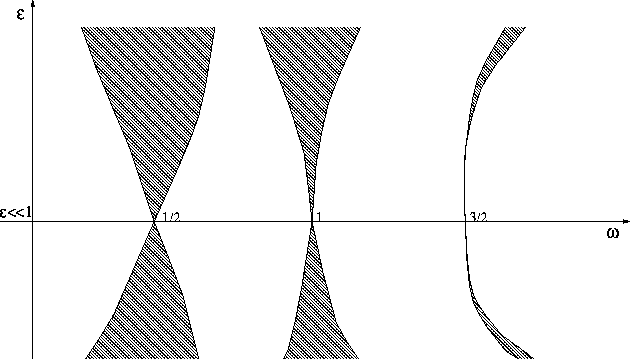
 , sono tratteggiate le zone di stabilità,
corrispondenti a |Tr B|<2.
, sono tratteggiate le zone di stabilità,
corrispondenti a |Tr B|<2. , con
, con 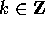 ) la posizione di equilibrio
inferiore è instabile: cioè una variazione periodica dei valori
dei parametri permette di dondolarsi sull'altalena. Il fenomeno è
detto della risonanza parametrica
) la posizione di equilibrio
inferiore è instabile: cioè una variazione periodica dei valori
dei parametri permette di dondolarsi sull'altalena. Il fenomeno è
detto della risonanza parametrica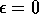 ), in
corrispondenza dei quali il problema è lineare e B può essere
esplicitamente calcolato:
), in
corrispondenza dei quali il problema è lineare e B può essere
esplicitamente calcolato:
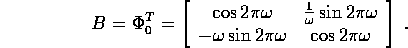
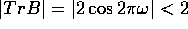 se
se 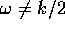 ; perciò il
dominio d'instabilità interseca l'asse
; perciò il
dominio d'instabilità interseca l'asse 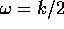 .
.